Многоканальная СМО с отказами (задача Эрланга)

Начнем рассмотрение с одной из простейших задач, которая возникла в начале 20 века при изучении работы телефонных станций. Изучалась эффективность работы телефонной станции, имеющей n каналов обслуживания (барышень, сидящих на коммутаторе). Все входящие потоки вызовов полагались простейшими. Интенсивность входного потока полагалась равной - 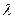Интенсивность обслуживания - .

Таким образом, СМО с отказами является такая система, в которой приходящие для обслуживания требования, в случае занятости всех каналов обслуживания, сразу ее покидают.

Найти:

- финальные вероятности

A- абсолютную пропускную способность

Q- относительную пропускную способность

- вероятность отказа

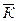- среднее число занятых каналов

если все n каналов заняты, то заявка получает отказ.

1. Введём множество состояний:

S0- все каналы пусты

S1- один канал занят

S2- два канала заняты

Sn- n каналов заняты.

2. Составим граф состояний:

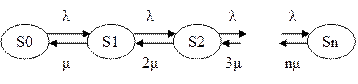
Обратите внимание на «разметку» нижних стрелок графа. Коэффициенты при интенсивности обслуживания возрастают с увеличением номера состояния. Это связано с тем, что если работают два канала, то обслужить свою заявку может каждый из них и суммарная интенсивность перехода в предыдущее состояние, где работает только один канал (любой из этих двух), равна , если работают три канала, то, соответственно, - и т.д.

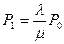
эти формулы называются формулами ЭРЛАНГА.

Q – относительная пропускная способность показывает вероятность того, что заявка будет обслужена.

,

где А - абсолютная пропускная способность есть поток на выходе системы в абсолютных величинах за единицу времени.

Пример. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Пусть среднее время работы с одним заказом составляет 3 часа. Интенсивность потока заявок 0,25 ч^-1. Найти вероятность отказа и среднее число занятых ЭВМ.

Имеем: m=3, l=0,25 ч^-1, =3 ч. Находим:

,

,

,

.

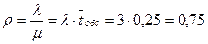Таким образом, ЭВМ.

Поиск по сайту: