Одноканальная СМО с неограниченной очередью (М/М/1)

Это одна из наиболее часто используемых моделей, относящихся к СМО с ожиданием. При ее рассмотрении принимаются следующие предположения:

- входной поток заявок (требований) - пуассоновский;

- время обслуживании распределено по экспоненциальному закону.

- среднее время обслуживания.

Найти:

- среднее время ожидания

U- среднее время пребывания

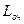- средняя длина очереди

N- среднее количество заявок в системе

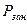- вероятность занятости устройства.

Будем определять характеристики этой СМО по уже рассмотренному в предыдущем случае алгоритму.

1. Введем множество состояний:

S0- канал (система) свободен

S1- одна заявка в СМО или канале и она обслуживается;

S2- две заявки в СМО - одна обслуживается, одна в очереди;

S3- три заявки в СМО – одна обслуживается, две в очереди;

Sn- n заявок в СМО – одна обслуживается, n-1 в очереди.

2.Составим граф состояний и разметим его.

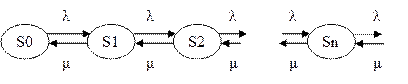
Для этой системы финальные вероятности существуют при 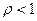, если .

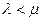Пр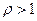и и 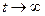очередь возрастает неограниченно.

При система справляется с потоком, если он регулярный.

3. По формулам для процесса гибели и размножения имеем:

; ; ;

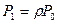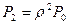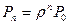Вероятность того, что система пуста: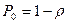

4. Определим характеристики эффективности

Среднее количество заявок в системе: …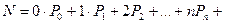

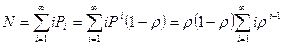
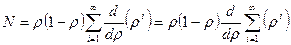
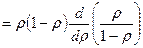
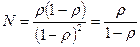
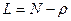
Вероятность занятости системы: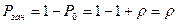

Среднее время ожидания заявок в очереди: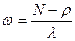

Поиск по сайту: