 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
СМО с ограниченным временем ожидания
В системах массового обслуживания с ограниченным временем ожидания время ожидания в очереди каждого требования ограничено случайной величиной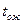 
, среднее значение которого 
.
Величина, обратная среднему времени ожидания, означает среднее количество требований, покидающих очередь в единицу времени, вызванное появлением в очереди одного требования: 
. Определение характеристик для этой СМО производится в той же последовательности, что и для систем рассмотренных выше, с той лишь разницей, что на размеченном графе к интенсивностям обработки прибавляются интенсивности ухода, связанные с превышением допустимого времени ожидания.
При наличии в очереди k требований интенсивность потока покидающих очередь требований составляет kn.
Для дальнейшего рассмотрения СМО с ограниченным временем ожидания введем новый параметр 
, означающий среднее число требований, покидающих систему необслуженными, приходящиеся на среднюю скорость обслуживания требований.
Формулы для определения вероятностей состояний такой системы имеют вид:
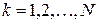, при 
;
, при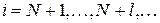 
,
где 
- произведение сомножителей 
.
Вероятность Р0 определяют по формуле
.
В практических задачах сумму бесконечного ряда вычислить достаточно просто, так как члены ряда быстро убывают с увеличением номера.
Средняя длина очереди:
.
Вероятность отказа:
.
Среднее число занятых каналов обслуживания и коэффициент загрузки:
;
.
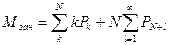Среднее число свободных каналов обслуживания и коэффициент простоя:
; 
.
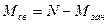Относительная пропускная способность
.
Пример. В пункте химчистки имеется три аппарата для чистки. Интенсивность потока посетителей l=6 посетителей в час. Интенсивность обслуживания посетителей одним аппаратом m=3 посетителей в час. Среднее количество посетителей, покидающих очередь, не дождавшись обслуживания, n=1 посетитель в час. Найти абсолютную пропускную способность пункта.
Имеем: m=З, l=6, m=3, n=1. Находим: 
,
.
Вероятность занятости всех приборов равна 
. Тогда абсолютная пропускная способность может быть получена как произведение: 
. Таким образом, А = 2,61 посетителя в час.
Контрольные вопросы к лекции 10
1. Объясните почему формулы выведенные для «схемы гибели и размножения» можно использовать и в случаях когда число состояний системы неограниченно.
2. Как ограничение времени ожидания в СМО отражается на графе состояний?
3. Изобразите граф состояний для системы типа М/М/2.
4. Запишите выражение для вероятности состояний Р3 СМО типа М/М/2
Поиск по сайту: