Задание 1. 1. Дан пуассоновский поток с параметром 2 мин-1

1. Дан пуассоновский поток с параметром 2 мин^-1. Найти вероятность того, что длина интервала между соседними требованиями составляет от 1 до 2 минут.

2. Производится наложение («суперпозиция») двух простейших потоков с интенсивностям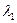и и 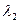. Будет ли поток, получившийся в результате наложения, простейшим, и если да, то с какой интенсивностью?

3. Производится случайное прореживание простейшего потока событий с интенсивностью 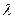; каждое событие, независимо от других, с вероятностью p сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате прореживания простейшего потока?

4. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 2 машины в минуту. Человек выходит на шоссе, чтобы остановить первую попавшуюся машину, идущую в данном направлении. Найти закон распределения времени Т, в течение которого ему придется ждать машину; определить математическое ожидание и среднее квадратичное отклонение.

5. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 4 машины в минуту. Шоссе имеет развилку в два направления. Вероятность движения машин в первом направлении равна 0,12, а во втором – 0,88. Определить интенсивности движения автомобилей в обоих направлениях.

6. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону 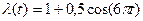. Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [1;9].

7. Компьютерный класс связан с каналом Интернет через 10-канальный концентратор. Интенсивности передачи данных по каждому из 10 каналов равны соответственно 540 бит/с, 120 бит/с, 40 бит/с, 170 бит/с, 350 бит/с, 60 бит/с, 742 бит/с, 153 бит/с, 500 бит/с, 100 бит/с. Поток данных подчиняется пуассоновскому закону распределения. Определить интенсивность передачи данных в канале Интернет.

8. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону 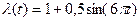. Параметр является периодическим, его период равен 1/4. Найти вероятность поступления одного, двух и трех требований.

9. Для простейшего потока с нестационарным параметром, определяемым равенством 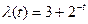, найти вероятность поступления двух требований на промежутке времени [3;8].

10. По железной дороге мимо наблюдателя движется в одном направлении простейший поток поездов. Известно, что вероятность отсутствия поездов в течение 10 минут равна 0,8. Требуется найти вероятность того, что за 20 мин мимо наблюдателя пройдет не более трех поездов.

11. Производится случайное прореживание простейшего потока событий с интенсивностью 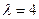; каждое событие, независимо от других, с вероятностью p=0,6 сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате прореживания простейшего потока?

12. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону 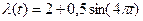. Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [1;5].

13. Дан пуассоновский поток с параметром 1 мин^-1. Найти вероятность того, что длина интервала между соседними требованиями составляет от 2 до 4 минут.

14. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 8 машин в минуту. Шоссе имеет развилку в три направления. Вероятность движения машин в первом направлении равна 0,12, во втором - 0,68, в третьем - 20. Определить интенсивности движения автомобилей во всех направлениях.

15. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 6 машин в минуту. Человек выходит на шоссе, чтобы остановить первую попавшуюся машину, идущую в данном направлении. Найти закон распределения времени Т, которое ему придется ждать; определить его математическое ожидание и среднее квадратичное отклонение.

16. Для простейшего потока с нестационарным параметром, определяемым равенством , найти вероятность поступления двух требований на промежутке времени [1;10].

17. В пункт текущего отделочного ремонта вагонов поступают требования на ремонт. Поток требований можно считать простейшим с интенсивностью 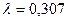. Найти вероятность того, что за час не поступит ни одного требования (вагона) на ремонт.

18. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону , где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 15 мин.

19. Для простейшего потока с нестационарным параметром, определяемым равенством 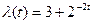, найти вероятность поступления двух требований на промежутке времени [2;6].

20. В пункт текущего отделочного ремонта вагонов поступает требование на ремонт. Поток требований можно считать простейшим с интенсивностью 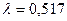. Найти вероятность того, что за час поступит одного требование (вагон) на ремонт.

21. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону 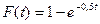, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 5 мин.

22. Производится случайное прореживание простейшего потока событий с интенсивностью 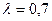; каждое событие, независимо от других, с вероятностью p=0,75 сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате прореживания простейшего потока?

23. Производится разбиение случайного простейшего потока событий с интенсивностью 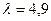на три потока. Вероятности попадания событий в тот или иной поток соответственно равны p₁=0,2, p₂=0,54, p₃=0,26. Определить интенсивности каждого получившегося потока в результате разбиения.

24. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону 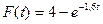, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 8 мин.

25. В пункт текущего отделочного ремонта вагонов поступают требования на ремонт. Поток требований можно считать простейшим с интенсивностью 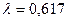. Найти вероятность того, что за час поступит одно требование (вагон) на ремонт.

26. Производится разбиение случайного простейшего потока событий с интенсивностью 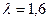на 2 потока. Вероятности попадания событий в тот или иной поток соответственно равны p₁=0,44, p₂=0,56. Определить интенсивности каждого получившегося в результате разбиения потока.

27. Компьютерный класс связан с каналом Интернет через 5-канальный концентратор. Интенсивности передачи данных по каждому из 10 каналов равны соответственно 541 бит/с, 110 бит/с, 44 бит/с, 171 бит/с, 356 бит/с. Поток данных подчинятся пуассоновскому закону распределения. Определить интенсивность передачи данных в канале Интернет.

28. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону 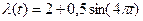. Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [4;9].

29. На вокзал прибывает пуассоновский поток поездов, в среднем 2 поезда за 5 минут. Найти вероятность того, что за 15 минут прибудут 3 поезда.

30. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону , где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 20 мин.

Поиск по сайту: