 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
При проектировании связано с системами массового обслуживания
Системы, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо видов услуг, а, с другой стороны, происходит удовлетворение этих запросов, называются системами массового обслуживания.
Система массового обслуживания включает следующие элементы: источник требований, входящий поток требований, очередь, обслуживающее устройство (обслуживающий аппарат, канал обслуживания), выходящий поток требований.
Системы массового обслуживания классифицируют по разным признакам. Одним из признаков является ожидание требования начала обслуживания. В соответствии с этим признаком системы подразделяются на следующие виды:
1) системы массового обслуживания с потерями (отказами);
2) системы массового обслуживания с ожиданием;
3) системы массового обслуживания с ограниченной длиной очереди;
4) системы массового обслуживания с ограниченным временем ожидания.
Системы массового обслуживания, у которых требования, поступающие в момент, когда все приборы обслуживания заняты, получают отказ и теряются, называются системами с потерями или отказами.
Системы массового обслуживания, у которых возможно появление как угодно длинной очереди требований к обслуживающему устройству, называются системами с ожиданием.
Системы массового обслуживания, допускающие очередь, но с ограниченным числом мест в ней, называются системами с ограниченной длиной очереди.
Системы массового обслуживания, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.
По числу каналов обслуживания СМО делятся на одноканальные и многоканальные.
По месту нахождения источника требований СМО делятся на разомкнутые, когда источник находится вне системы, и замкнутые, когда источник находится в самой системе. К последнему виду относится, например, станочный участок, в котором станки являются источником неисправностей, а следовательно, и требований на их обслуживание.
Одной из форм классификации систем массового обслуживания является кодовая (символьная) классификация Д. Кендалла. При этой классификации характеристику системы записывают в виде трех, четырех или пяти символов, например А | B | S, где А — тип распределения входящего потока требований, В — тип распределения времени обслуживания, S — число каналов обслуживания.
Для экспоненциального распределения принимают символ М, для любого (произвольного) распределения - символ G. Запись М | М | 3 означает, что входящий поток требований пуассоновский (простейший), время обслуживания распределено по экспоненциальному закону, в системе имеется три канала обслуживания.
Четвертый символ указывает допустимую длину очереди, а пятый — порядок отбора (приоритета) требований.
Уравнение Колмогорова для вероятностей состояний. Системы, представляемые в виде непрерывной цепи Маркова, обычно исследуют с помощью уравнения Колмогорова для вероятностей состояний.
Плотностью вероятности перехода  из состояния Si в состоянии Sj называется предел отношения вероятности этого перехода за время
из состояния Si в состоянии Sj называется предел отношения вероятности этого перехода за время  к длине промежутка
к длине промежутка  , когда последний стремится к нулю:
, когда последний стремится к нулю:
 ,
,
где  - вероятность того, что система, находившаяся в момент
- вероятность того, что система, находившаяся в момент  в состоянии Si, за время
в состоянии Si, за время  перейдет в состояние Sj.
перейдет в состояние Sj.
Марковская непрерывная цепь называется однородной, если плотность вероятностей  не зависит от времени
не зависит от времени  , в противном случае она называется неоднородной.
, в противном случае она называется неоднородной.
Для однородных Марковских непрерывных цепей, характеризующих процессы гибели и размножения, уравнения Колмогорова имеют вид:

 ,
,
где  - вероятность состояния Si, когда в системе находится
- вероятность состояния Si, когда в системе находится  требований в момент времени
требований в момент времени  ;
;  - общее число возможных состояний S0, S1,…, Sn.
- общее число возможных состояний S0, S1,…, Sn.
При гипотезе о стационарном режиме работы системы (вероятности состояний не зависят от времени) уравнения Колмогорова принимают вид:

В большинстве практических задач оказывается допустимой гипотеза о стационарном режиме работы системы. Поэтому могут быть использованы уравнения Колмогорова второго вида.
Пример
Пусть задана система, описываемая графом состояний S1,S2,S3,S4 и возможными переходами между ними

Каждому из этих состояний S1,S2,S3,S4 соответствует своя вероятность, что система будет в этом состоянии.
 - вероятность того, что система в момент времени t находится в состоянии S1.
- вероятность того, что система в момент времени t находится в состоянии S1.

Интенсивность переходов: 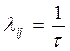 где
где  - время нахождения системы в данном состоянии.
- время нахождения системы в данном состоянии.
Зададим малое приращение  и найдем вероятность
и найдем вероятность  того, что в момент
того, что в момент  система будет находиться в состоянии S1.
система будет находиться в состоянии S1.
1. Система была в момент времени t в состоянии S1 и за время  никуда из этого состояния не ушла.
никуда из этого состояния не ушла.
2. В момент времени t система была в состоянии S2 и за время  перешла в состояние S1.
перешла в состояние S1.
Рассмотрим вероятности этих состояний:
1. 
2. 




Возьмем предел от этой функции:


Таким образом, система уравнений Колмогорова имеет вид:

Поиск по сайту: