Задачи из теории массового обслуживания

Сведения из теории вероятностей

1. Пусть – случайная величина и – некоторое её численное значение. Вероятность того, что примет значение, меньшее, чем , называют функцией распределения вероятностей случайной величины и символически пишут:

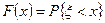. (4.6.1)

В дальнейшем будем предполагать, что F (x) дифференцируемая функция.

Функция , связанная с 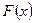равенством 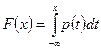, называется плотностью распределения вероятностей случайной величины . Очевидно

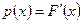. (4.6.2)

По определению, вероятность может принимать лишь значения . Отсюда следует, что функция распределения 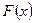является неотрицательной, ограниченной и, согласно (4.6.1) неубывающей функцией, а плотность – неотрицательна.

2. Плотность распределения суммы 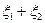двух независимых случайных величин 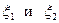, непрерывно распределенных с плотностями соответственно равна свертке плотностей

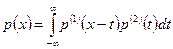, (4.6.3)

и равна дискретной свертке

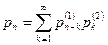
(4.6.4)

когда распределения слагаемых дискретны.

В случае если плотности имеют в отдельных точках разрывы 1-го рода, в формуле (4.6.3), кроме интегрального члена, появляются ещё дискретные слагаемые, соответствующие разрывам плотности.

3. На практике часто приходится иметь дело со случайными величинами, способными принимать лишь неотрицательные значения. Тогда 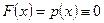при . Следовательно, функция распределения и плотность распределения в этом случае представляют собой правые односторонние функции, а их преобразования Фурье (характеристические функции) являются краевыми значениями функций, аналитических в верхней полуплоскости. Начало координат здесь, как правило, является точкой разрыва плотности и (при условии, что нет других разрывов) формула (4.6.3) принимает вид

. (4.6.5)

Среднее время пребывания в очереди.

Пусть в моменты времени в систему поступают требования на обслуживание. Введём следующие обозначения: − промежуток времени между поступлениями двух соседних требований, − длительность обслуживания r- го клиента, - длительность ожидания обслуживания.

Из простых соображений вытекает соотношение

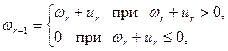(4.6.6)

где . (4.6.7)

Пусть 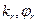– плотности распределения соответственно величин 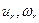. Очевидно, при . Считаем, что при 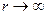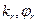имеют определённые пределы 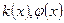. Из равенств (4.6.6) и (4.6.5) переходом к пределу при 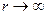получаем для определения интегральное уравнение Винера – Хопфа:

(4.6.8)

Решаем его следующим образом. Заменяем на , доопределяем уравнение на отрицательной полуоси внесением в правую часть произвольной левой односторонней функции и берём от обеих частей равенства преобразование Фурье. Получаем краевую задачу Римана относительно

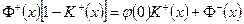(4.6.9)

в классе функций, исчезающих на бесконечности.

Переходя к исследованию полученной краевой задачи, заметим, что, так как величина 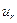, согласно (4.6.7), представляет собой алгебраическую сумму двух случайных величин , , 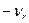то её плотность распределения 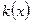будет сверткой плотностей слагаемых 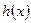, , 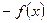соответственно:

В качестве 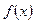можно взять плотность наиболее распространённого показательного закона, описывающего распределение величины промежутка времени между соседними событиями Пуассоновского потока Тогда

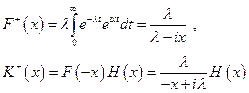
и краевое уравнение примет вид

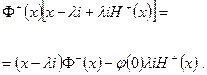
(4.6.10)

Так как коэффициент и свободный член краевого условия аналитически продолжимы в комплексную плоскость, то решать будем способом аналитического продолжения без обращения к общим формулам. Не указывая точного значения функции , используем лишь два её очевидных свойства:

Отсюда следует, что (других нулей на оси, как легко показать, нет), и так как , то коэффициент задачи Римана (4.6.10) имеет индекс единицу и полюс на контуре интегрирования в начале координат. Следовательно, имеем дело с исключительным случаем. По теореме Лиувилля имеем

откуда следует, что

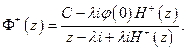
Определяя произвольную постоянную С из условия ограниченности решения в начале координат, получим , получаем

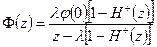. (4.6.11)

Постоянную 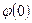здесь можно определить из равенства .

Формула (4.6.11) позволяет вычислить искомое среднее время ожидания, а также другие представляющие интерес характеристик распределения (математическое ожидание, дисперсию и т. д.).

Вероятность наличия в обслуживающей системе n требований.

Обозначим через вероятности того, что в обслуживающей системе в момент времени t находится n требований (n =0,1,2,….). Для определения этих вероятностей составим систему линейных дифференциальных уравнений Колмогорова

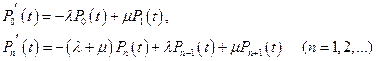(4.6.12)

где - постоянные коэффициенты, равные интенсивностям потоков, переводящих систему из состояния в состояние (рисунок 4.1).

Рисунок 4.1.

Эта система достаточно известна – она, служит математической моделью для обширного класса задач, известных под названием процессов размножения и гибели. Поэтому, не останавливаясь на ее выводе, сразу перейдем к решению системы (4.6.12).

Примем, что в начальный момент в обслуживающей системе находится l требований, то есть

(4.6.12′)

последние равенства при решении системы (4.6.12) будут служить начальными условиями.

Представляя правые стороны уравнений (4.6.12) в виде дискретной свертки (4.6.4), запишем систему в виде

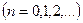(4.6.13)

где при и при .

Для решения системы используем приемы решения дискретных уравнений свертки. Доопределяем равенства (4.6.13) на отрицательные значения индекса п путем прибавления к правой части произвольной после­довательности 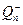(п = — 1, —2,...), затем умножаем все уравнения на со­ответствующие степени z и суммируем по всем п = 0, ±1,... (преобразование Лорана). После некоторых несложных преобразований получим равенство

(4.6.14)

где – производная функция для последовательности . В силу вероятностных соображений ограничена, поэтому аналитична в единичном круге. Произвольная последовательность 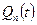(n =-1,-2,…) берется такой, чтобы 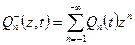была аналитичной вне единичного круга.

Соотношение (4.6.14) представляет собой на единичной окружности краевую задачу типа задачи Римана. Умножая (4.6.14) на z, и применяя теорему об аналитическом продолжении и теорему Лиувилля, получим

.

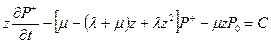Положив z= 0, имеем

.

Для отыскания остается решить линейное дифференциальное уравнение

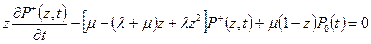(4.6.15)

при начальном условии (4.6.12′), т.е. при . Искомые вероятности находятся как коэффициенты ряда Тейлора по формулам .

Рассмотренные задачи, характеризуемые наличием одного канала обслужива­ния и равными возможностями клиентов, принадлежат к числу простейших. Более сложный класс задач − хотя и с одним обслуживающим каналом, но с предпочтением, отдаваемым отдельным видам требований («приоритет­ные задачи»), – приводит к краевой задаче Римана для функций также одного пере­менного, но зависящих от ряда параметров. Многоканальное обслуживание при наличии различных требований приводит к краевым задачам для функ­ций многих переменных.

Вопросы для оценки «остаточных» знаний

1. Аналитические функции и их свойства.

2. Преобразование Фурье с комплексным параметром.

3. Лемма Римана-Лебега.

4. Функции распределения вероятностей.

5. Уравнение Винера-Хопфа.

6. Краевая задача Римана.

7. Преобразование Лорана.

8. Дайте определение понятию «контроллинг».

9. Какие исходные данные должны быть определены предварительно для выработки оперативных УР.

10. Приведите пример экономических задач массового обслуживания.

Поиск по сайту: