Преобразование Фурье с комплексным параметром

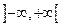Пусть функция задана в промежутке и удовлетворяет условиям теоремы 1:

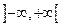Пусть функция определена в промежутке и удовлетворяет следующим условиям.

1⁰. Функция − кусочно непрерывна и имеет ограниченное изменение в любой конечной части промежутка ;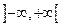

2⁰ . Функция абсолютно интегрируема в промежутке 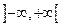. Тогда функция может быть представлена в виде разложения в интеграл Фурье:

где внешний интеграл понимается в смысле главного значения по Коши, причем в точке разрыва первого рода 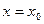левая часть этой формулы должна быть заменена подсуммой .

или теоремы 2:

Если функция имеет ограниченное изменение во всем бесконечном промежутке 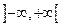и, сверх того, выполняется предельное равенство , где 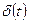- дельта-функция Дирака, то в каждой точке интеграл Фурье сходится и имеет значение .

Тогда имеет место интегральная формула Фурье , и, следовательно,

(4.5.1)

.

Пусть

(4.5.2)

Пусть, кроме того, , если , и ,если .

Рассмотрим интегралы

, (4.5.3)

, (4.5.4)

где .

Заметим, что интеграл (4.5.3) (или (4.5.4)) является несобственным интегралом, зависящим от переменной 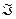как от параметра. Очевидно, что интеграл (4.5.3) (или (4.5.4)), вообще говоря, сходится не при всех значениях параметра .

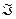Имеет место

Теорема 3. Пусть функция удовлетворяет следующим условиям.

1⁰. Функция кусочно непрерывна и имеет ограниченное изменение в любой конечной части промежутка

2⁰. Функция абсолютно интегрируема в промежутке

3⁰. Функция , если .

Тогда

1) если 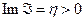, то функция , определяемая формулой (4.5.3), является аналитической функцией в верхней полуплоскости 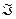- плоскости, причем в этой области она стремится к нулю при равномерно относительно ;

2) если 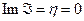, то функция является непрерывной функцией по и стремится к нулю при .

3) справедливо равенство

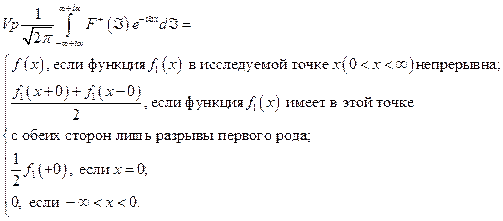(4.5.5)

где интеграл берется вдоль любой прямой , параллельной действительной оси 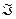- плоскости.

Доказательство. Первая часть первого утверждения данной теоремы следует из:

1) из равномерной сходимости интеграла (4.5.3) для любого , ибо он в силу условия 2⁰ мажорируется сходящимся интегралом:

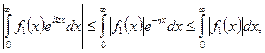
не содержащим параметра ;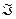

2) равномерной сходимости интеграла

где – любое натуральное число, для любого , поскольку этот интеграл в силу условия 2⁰ мажорируется сходящимся интегралом:

для любого .

Так как функция в любой точке полуплоскости 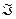-плоскости обладает производной любого порядка , то она является аналитической функцией в этой полуплоскости. Действительно, представив функцию в виде

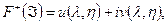
где

(4.5.6)

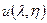и вычислив производные убедимся в том, что функции и являются гармоническими функциями, удовлетворяющими условиям Коши- Римана:

.

Следовательно, функция является аналитической функцией в полуплоскости 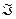-плоскости.

Из (4.1.6) видно, что функци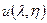и и стремятся к нулю при в любом случае (если, например, 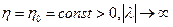, то и стремятся к нулю в силу добавления к первой основной лемме – лемме Римана-Лебега, так как функция с учетом условия 2⁰ является абсолютно интегрируемой функцией в промежутке ).

Первое утверждение данной теоремы доказано.

Второе утверждение данной теоремы доказано в книге В. Д. Кулиева «Сингулярные краевые задачи».

Теперь докажем справедливость равенства (4.5.5).

С помощью (4.5.3) и (4.5.6) получаем

(4.5.7)

Пусть . В этом случае в силу добавления к первой основной лемме – лемме Римана-Лебега, из (4.5.7) получаем

(4.5.8)

Пусть . В этом случае из (4.5.7) получаем

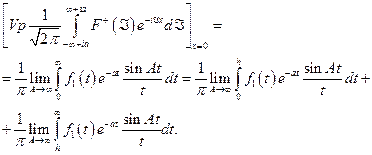(4.5.9)

Второе слагаемое в (4.5.9) равно нулю в силу добавления к первой основной лемме – лемме Римана-Лебега.

Замечая, что функция имеет ограниченное изменение в промежутке , с помощью второй основной леммы Дирихле – и утверждения: для того, чтобы функция 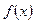имела в промежутке ограниченное изменение, необходимо и достаточно, чтобы она представлялась в этом промежутке в виде разности двух монотонно возрастающих и ограниченных функций: , (в силу второй основной леммы – леммы Дирихле – и утверждения).

находим

Следовательно,

(4.5.10)

Пусть . В этом случае формулу (4.5.7) представим в виде

. (4.5.11)

Пусть . Формулу (4.5.11) можно записать в виде

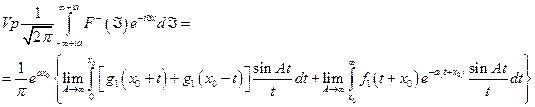(4.5.12)

Здесь .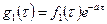

Функция имеет ограниченное изменение в промежутке с центром в точке . Замечая, что второе выражение (в силу добавления к первой основной лемме – лемме Римана-Лебега) в (4.5.12) равно нулю, и учитывая, что

(в силу первой основной леммы – леммы Римана-Лебега) равенство (4.5.12) можно записать в виде

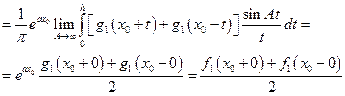(4.5.13)

Если функция в исследуемой точке непрерывна, то

(4.5.14)

Полученные результаты (4.5.8), (4.5.10), (4.5.13) и (4.5.14) доказывают справедливость равенства (4.5.5).

Теорема 3 доказана.

Теорема 4. Пусть функция удовлетворяет следующим условиям.

1⁰. Функция кусочно непрерывна и имеет ограниченное изменение в любой конечной части промежутка ;

2⁰. Функция абсолютно интегрируема в промежутке ;

3⁰. Функция , если .

Тогда

1. если , то функция 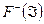, определяемая формулой (4.5.4), является аналитической функцией в нижней полуплоскости 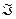- плоскости, причем в этой области она стремится к нулю при равномерно относительно .

2. если , то функция является непрерывной функцией по и стремится к нулю при .

3. справедливо равенство

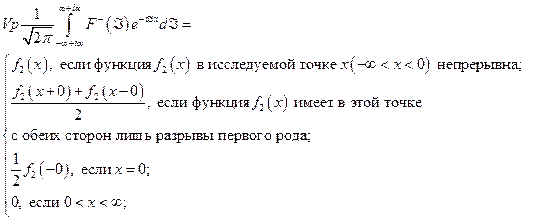
где интегрирование производится по любой прямой , параллельной действительной оси 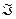- плоскости.

Доказательство аналогично доказательству теоремы 3.

Теорема 5. Положим

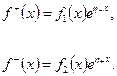
Пусть функции и удовлетворяют условиям 1⁰, 3⁰ теоремы 3 и теоремы 4 соответственно. Кроме того, условие 2⁰ в теореме 3 заменим на условие

при

а в теореме 4 – на условие

при .

Тогда

1. Функция , определяемая формулой

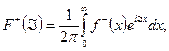
является аналитической функцией комплексной переменной в области , причем в этой области она стремится к нулю при равномерно относительно .

2. Справедливо равенство

где интеграл берется вдоль любой прямой 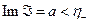, параллельной действительной оси 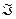- плоскости.

3. Функция 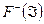, определяемая формулой

является аналитической функцией комплексной переменной в области , причем в этой области она стремится к нулю при равномерно относительно .

4. Справедливо равенство

где интеграл берется вдоль любой прямой , параллельной действительной оси 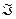- плоскости.

5. Если то функция

где

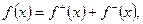
является аналитической функцией комплексной переменной в полосе

6. В любой точке непрерывности функции 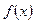справедливо равенство

,

а в любой точке разрыва первого рода функции 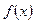- равенство

где интегрирование в последних двух формулах производится по любой прямой, параллельной действительной оси 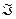- плоскости, лежащей в полосе 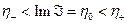, и понимается в смысле главного значения. В частности, пр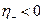и и функция является аналитической в полосе , содержащей действительную ось 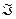- плоскости.

Только что сформулированная теорема имеет большое практическое значение при решении различных краевых задач уравнений математической физики.

В качестве примера рассмотрим интегральное уравнение Винера-Хопфа

(4.5.15)

ядро которого, функция зависит от разности и определено для всех значений своего аргумента .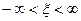

Покажем, что решение этого интегрального уравнения с помощью теоремы 5 сводится к решению функционального уравнения Винера-Хопфа.

Введём функции

(4.5.16)

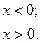
Уравнение (4.5.15), согласно (4.5.16), можно записать в виде

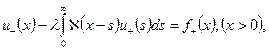(4.5.17)

(4.5.18)

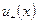Функция определяется из решения интегрального уравнения (4.5.17), а выражается через функции , и 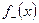с помощью квадратурной формулы (4.5.18). При этом имеет место соотношение

, (4.5.19)

эквивалентное исходному уравнению (4.5.15).

Пусть функция 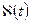удовлетворяет условиям

при

(4.5.20)

при

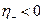где и . Тогда функция

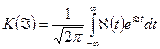
в силу теоремы 5 будет аналитической в полосе , .

Кроме того, пусть

при

(4.5.21)

при

где , . Тогда функция

в силу этой же теоремы будет аналитической в полосе , .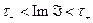

Для определенности положим, что . Будем искать решение уравнения (4.5.15), удовлетворяющее условию

при (4.5.22)

где 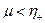, не останавливаясь на доказательстве существования решения уравнения (4.5.17), обладающего указанным свойством. При этом интегралы в формулах (4.5.17) и (4.5.18) являются сходящимися, причем для функции 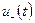имеет место оценка

при (4.5.23)

что легко получается из (4.5.18).

Из (4.5.22) и (4.5.23) следует, что преобразования Фурье

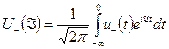
функци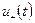и и 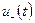в силу теорем 3, 4 являются аналитическими функциями комплексной переменной 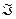при и 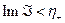соответственно, а функция

аналитична в полосе , .

Для определенности положим, что .

Умножив (4.5.15) на и проинтегрировав по от до , получаем

(4.5.24)

Изменив в последнем слагаемом порядок интегрирования, представим этот интеграл в виде

.

Сделаем замену переменной интегрирования, положив .

Тогда

(4.5.25)

где

.

Поиск по сайту: