 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема Жордана
Каждая замкнутая жорданова кривая делит плоскость на две различные области, для которых она является общей границей.
2. Понятие комплексного интегрирования. Пусть 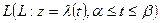 - спрямляемая кривая и
- спрямляемая кривая и 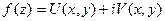 - функция, определенная и непрерывная на
- функция, определенная и непрерывная на  .
.
Так как криволинейные интегралы
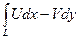 ,
, 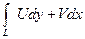
существуют, то существует и выражение вида
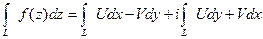 . (4.3.1)
. (4.3.1)
Этот интеграл называют комплексным интегралом.
Из (4.3.1) следует, что на интегралы от функций комплексного переменного распространяются обычные свойства криволинейных интегралов второго типа:
1) 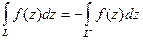 (4.3.2)
(4.3.2)
Здесь через 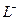 обозначается кривая, отличающаяся от
обозначается кривая, отличающаяся от  только направлением обхода.
только направлением обхода.
2) 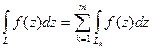 (4.3.3)
(4.3.3)
Здесь 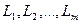 - дуги, получающиеся при каком-либо разбиении кривой
- дуги, получающиеся при каком-либо разбиении кривой  на части, причем начало дуги
на части, причем начало дуги 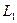 совпадает с началом кривой
совпадает с началом кривой  , начало дуги
, начало дуги  - с концом дуги
- с концом дуги 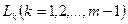 и конец дуги
и конец дуги 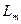 - с концом кривой
- с концом кривой  .
.
3) 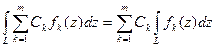 (4.3.4)
(4.3.4)
Здесь 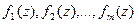 - функции, определенные и непрерывные на
- функции, определенные и непрерывные на  , а
, а 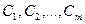 - комплексные постоянные.
- комплексные постоянные.
4) Если 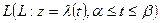 - кусочно-гладкая кривая, то
- кусочно-гладкая кривая, то
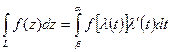 (4.3.5)
(4.3.5)
5)  , (4.3.6)
, (4.3.6)
где  - длина кривой
- длина кривой  . Чтобы получить это неравенство, достаточно заметить, что
. Чтобы получить это неравенство, достаточно заметить, что
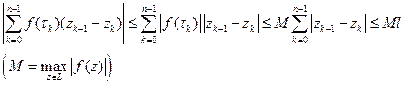
и перейти к пределу.
Все перечисленные свойства являются точными аналогами соответствующих свойств интегралов от действительных функций.
Однако необходимо отметить, что одно из свойств определенных интегралов от действительных непрерывных функций (так называется первая теорема о среднем значении) не имеет места для определенных интегралов от комплексных непрерывных функций даже в том случае, если ограничиться интегрированием вдоль отрезка действительной оси.
3. Формула Римана-Грина. Как известно, формула Грина
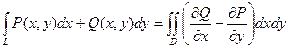 (4.3.7)
(4.3.7)
где  - внутренность замкнутой жордановой кривой
- внутренность замкнутой жордановой кривой  , выводится обычно при следующих предположениях:
, выводится обычно при следующих предположениях:
а) любая прямая, параллельная координатной оси, пересекает  не более, чем в двух точках (исключения допускаются только для двух крайних положений в направлении каждой оси, где возможно пересечение по прямолинейному отрезку);
не более, чем в двух точках (исключения допускаются только для двух крайних положений в направлении каждой оси, где возможно пересечение по прямолинейному отрезку);
б) функции 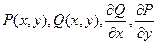 непрерывны в замкнутой области
непрерывны в замкнутой области 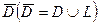 .
.
В формуле (4.3.7) криволинейный интеграл берется в положительном направлении, то есть в направлении против часовой стрелки.
Имеет место
Утверждение. Пусть  - внутренность замкнутой жордановой кусочно-гладкой кривой
- внутренность замкнутой жордановой кусочно-гладкой кривой  и пусть действительная и мнимая части
и пусть действительная и мнимая части 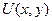 и
и  функции
функции 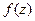 непрерывны и обладают в замкнутой области
непрерывны и обладают в замкнутой области 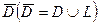 непрерывными частными производными первого порядка. Тогда
непрерывными частными производными первого порядка. Тогда
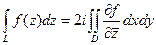 (4.3.8)
(4.3.8)
Действительно, в силу формулы (4.2.2),(4.3.1) и (4.3.7) имеем
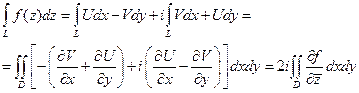 (4.3.9)
(4.3.9)
Формулу (4.3.8) называют формулой Римана-Грина.
Поиск по сайту: