 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Далее приводится пример построения сетевого графа и расчет его временных параметров
1. По исходным данным (таблица 3.6) построить сетевой граф и закодировать его работы. Максимальное количество источников ресурса  .
.
Таблица 3.6.
Исходные данные для расчета параметров сетевого графа
| l–i | i–j | t (i-j) | P (i-j) |
| - | а | ||
| - | б | ||
| - | в | ||
| в, а | г | ||
| а | д | ||
| д, в | е | ||
| в | ж | ||
| б, д, е | з |
 |
Построение сетевого графа и кодирование его событий и работ
2. Расчет временных параметров сетевого графа. Временные параметры, характеризующие работы сетевого графа, рассчитываются по приведенным выше расчетным формулам. Это следующие параметры:
 ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
,  ,
,  .
.
 |
 = 19: (1-2), (2-4), (4-6), (6-7), (7-8).
= 19: (1-2), (2-4), (4-6), (6-7), (7-8).
Критический путь на сетевом графе выделяется, например, двойной линией, более жирной (рисунок 3.13) и т.п.

Рисунок 3.13. Критический путь сетевого графа
3. Расчет временных параметров сетевого графа в табличной форме (таблица 3.7).
Таблица 3.7.
Расчетные параметры сетевого графа
| J | 
| 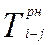
| 
| 
| 
| 
| 
| 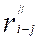
|
| 1-2 1-3 1-7 2-4 2-5 3-5 3-6 3-8 4-6 4-7 5-8 6-7 7-8 |
4. Привязка сетевого графа к календарю. При выполнении работ сетевого графа существенную роль играет их временная регламентация. Отсюда, необходимость привязки работ графа к временной шкале. Эта процедура может носить строго целевой характер, то есть быть ориентирована на жесткую привязку работ к конкретным календарным датам, а может носить нормативный характер, предусматривающий привязку работ к гипотетическому вектору, неориентируемому на строгие календарные даты. Тогда такое расписание выполнения работ, необходимых для разработки управленческого решения, может быть встроено в любой календарный график, и таким образом, гипотетическая структура станет реальным оперативным планом выполнения конкретных работ.
Привязка работ сетевого графа к календарю (рисунок 3.14) предусматривает реализацию следующего комплекса процедур:
1. Построение на плоскости временной шкалы в виде вектора (горизонтальной прямой), на которой откладываются временные отрезки, суммарная величина которых равна продолжительности критического пути (интервалы временной шкалы соответствуют единицам измерения параметров сетевого графа).
2. Выбор работ критического пути и последовательное их наложение на построенную временную шкалу с указанием номеров соответствующих событий.
3. Отображение в виде отрезков, наклоненных к временной шкале или параллельных ей, работ и событий, не принадлежащих критическому пути, на плоскости построенного вектора по следующим правилам:
· из каждого события, лежащего на критическом пути, под любым углом к временной шкале провести прямые, на каждой из которых отложить соответствующую ( ) работу, выходящую из этого события или входящую в него; указать начальное и конечное событие этих работ. Проекция работы на временную шкалу должна быть равна ее продолжительности (
) работу, выходящую из этого события или входящую в него; указать начальное и конечное событие этих работ. Проекция работы на временную шкалу должна быть равна ее продолжительности (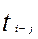 );
);
· выбор работы ( ) события, которой
) события, которой 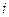 и
и  не принадлежат критическому пути, и при формировании ее к конечному событию непосредственно предшествующей работы по правилам, изложенным в п.3.1.
не принадлежат критическому пути, и при формировании ее к конечному событию непосредственно предшествующей работы по правилам, изложенным в п.3.1.
Такие процедуры произвести со всеми без исключения работами сетевого графа, события которых не принадлежат  .
.
· работы сетевого графа, не лежащие на критическом пути, можно отобразить как над временной шкалой, так и под ней, стараясь обеспечить наиболее простое восприятие построенной эпюры.
Примечание:
фиктивные работы не требуют для своего выполнения затрат времени, поэтому их проекция на временную шкалу равна нулю, и, следовательно, фиктивные работы будут формироваться на перпендикуляре к тому событию, из которого выходит фиктивная работа; если фиктивная работа принадлежит критическому пути, то начальное и конечное события на временной шкале совмещаются;
4. В случае, когда одно и то же событие является конечным для нескольких работ, не лежащих на критическом пути, и продолжительность их выполнения различна, то все эти работы следует заканчивать фиктивным событием, которое должно нумероваться одним и тем же порядковым номером с соответствующим индексом (а, б, в и т.д. или ,, ,,, ,,, и т.д.), который устанавливается по мере привязки работ к временной шкале на строящейся эпюре. Эти номера конечных событий (одинаковые по порядковому номеру, но различные по индексу) соединяются последовательно штриховыми линиями, проекция которых на временную шкалу соответствует по величине резерву времени второго вида  .
.
5. При наличии у сетевого графа более одного критического пути, последовательно строится такое количество временных шкал, сколько есть критических путей. Эти временные шкалы на плоскости располагаются параллельно, а начальная и конечная точки отсчета располагаются на одной вертикали. Привязка работ к этим дополнительным временным шкалам (построение эпюр) осуществляется в описанном выше порядке. Расстояние между временными шкалами выбирается с учетом количества работ, связанных с событиями, находящимися на соответствующем критическом пути.

Рисунок 3.14. Привязка сетевого графа к календарю
Закрепление работ сетевого графа за ресурсами и формирование расписания их выполнения.
Для выполнения работ сетевого графа требуется наличие одного или нескольких видов ресурсов. Если учитывается только один вид ресурса, например, имеющийся в наличии персонал, пропускная способность оборудования и т. п., то правомерно говорить об одноресурсной модели. Если ресурсов несколько, имеем дело с многоресурсной моделью. Поскольку имеющиеся в наличии ресурсы ограничены, возникает проблема оптимального закрепления работ сетевого графа за имеющимися ресурсами, т.е. оптимального или хотя бы рационального их использования, так как тот или иной вариант закрепления работ за источниками ресурсов будет определять общую продолжительность выполнения работ сетевого графа.
Наименьшая продолжительность выполнения всех работ сетевого графа равна критическому пути ( ). За это время могут быть выполнены все работы графа при условии неограниченности ресурсов, либо в случае, когда потребность в источниках ресурсов для выполнения соответствующих работ в каждый момент времени меньше или равна имеющемуся в наличии их количеству. Если фактическое количество источников ресурсов меньше потребного, то возникает вопрос выбора наиболее рационального варианта последовательности выполнения работ сетевого графа, т.е. установления их определенной очередности, следовательно имеет место вариантная оптимизационная задача.
). За это время могут быть выполнены все работы графа при условии неограниченности ресурсов, либо в случае, когда потребность в источниках ресурсов для выполнения соответствующих работ в каждый момент времени меньше или равна имеющемуся в наличии их количеству. Если фактическое количество источников ресурсов меньше потребного, то возникает вопрос выбора наиболее рационального варианта последовательности выполнения работ сетевого графа, т.е. установления их определенной очередности, следовательно имеет место вариантная оптимизационная задача.
Решение такого класса задач требует использования системы критериальных и ограничительных условий. В качестве таких критериальных условий могут быть:
1) первоочередное включение в график загрузки источников ресурса (при графической интерпретации использования ресурсов) фиктивных работ, поскольку они открывают возможность выполнения новых работ графа, а сами не требуют ни расходования ресурса, ни трудозатрат;
2) первоочередность выполнения работ, принадлежащих критическому пути;
3) первоочередность выполнения работ, имеющих наибольшую трудоемкость;
4) первоочередность выполнения работ, имеющих наименьшую трудоемкость;
5) первоочередность выполнения работ, требующих наименьшего (наибольшего) количества источников ресурсов;
6) первоочередность выбора работ, выполнение которых позволит наиболее полно использовать имеющиеся на данный момент времени ресурсы и т.п.
Кроме того, может быть выбрана любая комбинация этих критериев, которая позволяет путем последовательного перебора выбрать для выполнения работу сетевого графа, наиболее приоритетную для сложившейся ситуации.
В качестве ограничительных условий могут выступать:
1) наличное количество источников ресурсов;
2) последовательность выполнения работ сетевого графа, то есть непосредственно следующие и следующие работы не могут быть выполнены не только ранее данной ( ), но и предшествующих ей (
), но и предшествующих ей (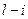 ) работ;
) работ;
3) общая потребность в источниках конкретного ресурса по всем одновременно выполняемым работам не может превышать фактическое наличие источников этого ресурса.
При построении графика закрепления работ сетевого графа за источниками ресурса необходимо выполнять ряд условий и соблюдать следующие требования:
· в качестве базы графической интерпретации закрепления работ сетевого графа за имеющимися источниками ресурса используется первая четверть системы координат, где по горизонтальной оси откладывается трудоемкость (продолжительность выполнения работ сетевого графа), а по вертикальной – количество имеющихся источников ресурса;
· в соответствии с очередностью выбора каждая работа на графике отображается в виде отрезков длиной, равной трудоемкости выполнения этой работы; число таких отрезков равно количеству источников ресурсов, требующихся для выполнения данной работы;
· при выполнении выбранной работы все требующиеся источники задействуются одновременно по началу выполнения работ и освобождаются также одновременно по истечении продолжительности выполнения данной работы, то есть если ресурс использован не полностью, но для выполнения очередной выбранной работы свободного ресурса недостаточно, то этот свободный источник (источники) не используется, пока не появится в какой-либо момент времени необходимое и достаточное количество этих источников ресурса для выполнения следующей по очереди работы графа; разрыв во времени выполнения конкретной работы не допускается;
· очередная работа сетевого графа может быть включена в график загрузки источников ресурсов, только если в него уже включены все работы, предшествующие данной;
· «фиктивные» работы строятся в виде пунктирной перпендикулярной линии, направленной вверх, так как их трудоемкость и потребный ресурс равны нулю;
При решении рассматриваемого примера в качестве критериальных условий следующие:
1) приоритетность выполнения работ, принадлежащих критическому пути:
 ;
;  ;
;
2) приоритетность выполнения работ, наиболее полно догружающих при прочих равных условиях имеющиеся свободные источники ресурса ( ):
):
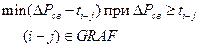 ;
;
3) приоритетность при прочих равных условиях выполнения работ, требующих наибольших трудозатрат:
 ,
, 
Рассмотрим следующие альтернативные варианты:
Пусть имеется в наличии один вид ресурса, представленный пятью источниками (по исходным данным таблицы 3.6 «Исходные данные для расчета параметров сетевого графа »). Претендентами на первоочередное выполнение являются работы, выходящие из события 1: (1-2), (1-3), (1-7). Из этого состава работ критическому пути принадлежит только работа (1-2). Согласно принятым критериям отбора работ для установления очередности их выполнения выбираем работу (1-2), то есть выбор сделан уже по первому из принятых критериальных условий:
 .
.
Для выполнения этой работы требуется пять источников ресурса, которые будут задействованы в течение пяти временных единиц (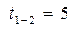 ) – рисунок 3.15.
) – рисунок 3.15.

Рисунок 3.15. Закрепление работы (1-2) за имеющимися источниками ресурса
После выполнения работы (1-2) появляется возможность выполнения, кроме работ (1-3) и (1-7), еще и работ (2-4) и (2-5), непосредственно следующих за работой (1-2). Согласно заданным критериальным условиям в первую очередь выбираем работу, принадлежащую критическому пути. Такой работой является работа (2-4):
 .
.
Предшествующие ей работы выполнены, следовательно, она может быть выбрана для загрузки ресурсов сетевого графа. Для выполнения этой работы требуется два источника ресурса в течение семи единиц ( ), эпюра загрузки ресурсов сетевого графа будет выглядеть следующим образом (рисунок 3.16):
), эпюра загрузки ресурсов сетевого графа будет выглядеть следующим образом (рисунок 3.16):

Рисунок 3.16. Закрепление работы (2-4) за имеющимися источниками ресурса
После выполнения работы (2-4) появляется возможность выполнения, кроме работ (1-3), (1-7), (2-5), еще и работ (4-6) и (4-7). Согласно заданным критериальным условиям в первую очередь выбираем работу, принадлежащую критическому пути. Такой работой является работа (4-6). Все предшествующие ей работы выполнены, следовательно, ей можно загрузить имеющиеся ресурсы:

Эта работа фиктивная, поэтому для ее выполнения не требуется ни источников ресурса, ни затрат времени. Работа (4-6) может выполняться только после наступления события 4, то есть после выполнения работы (2-4) – рисунок 3.17:

Рисунок 3.17. Закрепление работы (4-6) за имеющимися источниками ресурса
На этом рисунке представлена эпюра загрузки ресурсов, имеющихся у организации для выполнения работ, сетевого графа после включения работы (4-6). Аналогичные построения ведутся по всем фиктивным работам сетевого графа с учетом изложенных выше методических положений.
После выполнения работы (4-6) дополнительных работ не открывается, так как единственная работа, выходящая из события 6, (6-7), не может быть выполнена без наступления этого события, а оно наступит только после выполнения работы (3-6).
Таким образом, к настоящему моменту в очереди на выполнение стоят следующие, оставшиеся от предыдущей операции работы – (1-3), (1-7), (2-5), (4-7). Из этих работ будем выбирать, последовательно перебирая объявленные критериальные условия, ту, которая будет соответствовать принятым условиям.
Ни одна из указанных работ не принадлежит  , следовательно по первому целевому критериальному условию работа не выбрана. Переходим ко второму критериальному условию.
, следовательно по первому целевому критериальному условию работа не выбрана. Переходим ко второму критериальному условию.
Свободный ресурс имеется на шестой момент времени и составляет три источника. Среди работ-претендентов на очередность выполнения выберем ту, которая соответствует второму критериальному условию и изложенным принципиальным положениям постоения графика загрузки источников ресурса:
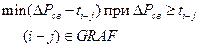 .
.
Условие соблюдается при выборе работы (1-3):

Выбираем работу (1-3).
Работа (1-3) не имеет предшествующих работ, следовательно, она может начинаться в любой момент времени, когда имеются свободные источники ресурса. В нашем случае три источника ресурса освободились на шестой временной единице. В этот момент и начнем выполнение данной работы (рисунок 3.18), требующий наличие как раз трех источников ресурса:

Рисунок 3.18. Закрепление работы (1-3) за имеющимися источниками ресурса
После выполнения работы (1-3) появляется возможность выполнения, кроме работ (1-7), (2-5), (4-7), еще и работ (3-5), (3-6) и (3-8). Это альтернативные варианты для установления очередности выполнения работ сетевого графа. Согласно заданным критериальным условиям в первую очередь выбираем работу, принадлежащую критическому пути. Такой работы среди перечисленных нет, следовательно, нужно обратиться ко второму критериальному условию.
Свободный ресурс имеется на тринадцатый момент времени и составляет два источника. Среди работ-претендентов на очередность выполнения выберем ту, которая соответствует второму критериальному условию: при  выбираем работу, максимально загружающую свободный ресурс, т.е. обеспечивающую минимальный недогруз (недоиспользование) имеющегося ресурса:
выбираем работу, максимально загружающую свободный ресурс, т.е. обеспечивающую минимальный недогруз (недоиспользование) имеющегося ресурса:

По второму критериальному условию:
 .
.
Имеем альтернативные варианты, так как обе эти работы (1-7) и (3-8) требуют для своего выполнения по два источника ресурса, то есть одинаково загружают имеющийся свободный резерв ресурса. В такой ситуации необходимо обратиться к третьему критерию, чтобы из альтернативных вариантов выбрать один в связи с ограниченностью ресурсов:  ,
,  .
.
 .
.
Таким образом, в результате перебора всех критериальных условий выбрана работа (1-7). Она не имеет предшествующих ей работ, следовательно, она может быть включена в график загрузки ресурсов сетевого графа в любой момент, когда имеется достаточный объем свободного ресурса (рисунок 3.19):

Рисунок 3.19. Закрепление работы (1-7) за имеющимися источниками ресурса
Выполнение работы (1-7) не открывает дополнительных работ-претендентов, включаемых в формируемую очередь. Следовательно, в очереди выполняемых работ остались работы (2-5), (3-5), (3-6), (3-8), (4-7).
Из этих работ, последовательно перебирая объявленные критериальные условия, будем выбирать соответствующую им. Как указывалось ранее, ни одна из этих работ не принадлежит критическому пути, следовательно, выбор работ осуществляем по 2-му критерию.
Свободный ресурс имеется на четырнадцатый момент времени и составляет три источника. Среди работ-претендентов на очередность выполнения выберем ту, которая соответствует второму критериальному условию: 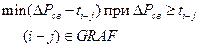 ,
,
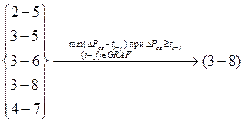 .
.
Такой работой является работа (3-8). Она не имеет незакрепленных за источниками ресурса предшествующих работ, поэтому может быть включена в составляемый график (эпюру) – рисунок 3.20:

Рисунок 3.20. Закрепление работы (3-8) за имеющимися источниками ресурса
Выполнение работы (3-8) не открывает дополнительных работ-претендентов, включаемых в формируемую очередь, так как она входит в конечное событие, из которого не выходит ни одной работы. Следовательно, в очереди выполняемых работ остались работы (2-5), (3-5), (3-6), (4-7).
Из этих работ будем выбирать, последовательно перебирая объявленные критериальные условия, ту, которая будет им соответствовать в наибольшей степени.
Свободный ресурс имеется на четырнадцатый момент времени и составляет один источник. Среди работ-претендентов на очередность выполнения выберем ту, которая соответствует второму критериальному условию: 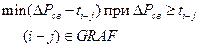 .
.
Все рассматриваемые работы фиктивные, следовательно, для каждой из них второе критериальное условие подходит в равной степени.
 .
.
Обращение к третьему критериальному условию:  , ситуацию не изменят, т.к. у всех фиктивных работ трудоемкость равна 0, т.е. трудозатраты по всем четырем работам равны по величине.
, ситуацию не изменят, т.к. у всех фиктивных работ трудоемкость равна 0, т.е. трудозатраты по всем четырем работам равны по величине.
Отработаны все критериальные условия, в результате чего выбраны четыре работы. Поскольку имеют место альтернативные варианты, следовало бы задаться четвертым критериальным условием, так как при реальном построении графика загрузки источников ресурса мы вышли за пределы заданных критериальных условий. Но наш вариант особенный: все указанные работы являются фиктивными, то есть не требуют для своего выполнения ни трудо-, ни других ресурсных затрат. Следовательно, их можно включить в формируемый график загрузки (отразить на эпюре загрузки) источников ресурса. Эту процедуру можно выполнить по изложенной ранее методике (см. рисунок 3.17 «Закрепление работы (4-6) за имеющимися источниками ресурса» и комментарии к нему).
Включение рассматриваемых фиктивных работ в эпюру загрузки источников ресурса можно начинать после выполнения всех работ, входящих в событие, являющееся начальным для фиктивной работы, не учитывая загрузку ресурсов, либо с учетом ее. Тогда выполнение работы (2-5) можно включать в график очередности либо после выполнения работы (1-2), либо после работы (1-3) на четырнадцатом моменте времени; работы (3-5), (3-6) после выполнения работы (1-3) либо (3-8) на восемнадцатой временной единице, а (4-7) после выполнения работы (2-4) либо (1-7) (рисунок 3.21). Ориентацию при включении фиктивных работ в разрабатываемую эпюру загрузки источников ресурса наличием хотя бы минимального свободного ресурса можно рассматривать как своего рода временного резерва, необходимого на подготовку для формирования следующих звеньев очереди выполнения работ, в том числе и требующих ресурсных затрат.

Рисунок 3.21. Один из вариантов включения фиктивных работ (2-5), (3-5), (3-6), (4-7) в эпюру загрузки имеющихся источников ресурса
После включения этих работ в эпюру загрузки источников ресурса появляется возможность выполнения работ (5-8) и (6-7). Выбор очередной работы осуществляется по правилам, изложенным ранее, с ориентацией на методические приемы, использовавшиеся при построении графика загрузки источников ресурса решаемого иллюстративного примера. Процедуры выбора работ для их закрепления за источниками ресурса ведутся до тех пор, пока не будут рассмотрены все работы сетевого графа. Наш вариант закрепления работ за источниками ресурса будет выглядеть следующим образом (рисунок 3.22):

Рисунок 3.22. Закрепление работ сетевого графа за имеющимися источниками ресурса
Нами рассмотрен пример жесткого задания критериальных условий при формировании очередности выполнения работ сетевого графа с учетом имеющегося источника ресурса.
Такой вариант решения данной задачи не единственно возможный. Может иметь место изменение состава критериальных условий непосредственно в процессе установления очередности выполнения работ. Такое изменение состава критериальных условий может осуществляться на основе заранее сформированного набора таких критериев выполнения каждой очередной итерации закрепления работ сетевого графа за источниками ресурса или после выполнения определенного комплекса работ сетевого графа. Использование такого подхода может быть продиктовано изменяющимися условиями решения задачи, логической оценкой целесообразности применения другого набора критериев и т.п.
После закрепления работ сетевого графа за источниками ресурса рассчитываются коэффициенты загрузки и простоя имеющихся ресурсов по формулам:

где  – время использования имеющихся ресурсов, устанавливаемое по эпюре их загрузки.
– время использования имеющихся ресурсов, устанавливаемое по эпюре их загрузки.
 = 1 –
= 1 – 
Для решаемого примера:


 = 1 – 0,857 = 0,143
= 1 – 0,857 = 0,143
Такой уровень использования (загрузки) источников ресурса можно считать удовлетворительным.
Далее представлен примерный состав работ по организационному обеспечению выполнения заказов, для оптимизации, которого можно использовать сетевой граф (таблица 3.8).
Таблица 3.8.
Состав работ сетевого графа по организационному обеспечению выполнения заказов
| № п/п | Работы по обеспечению выполнения заказов |
| Маркетинговое исследование рынка | |
| Предварительная работа с потенциальными заказчиками | |
| Предварительная работа по формированию портфеля заказов | |
| Предварительные технико-экономические расчеты по потенциальным заказам | |
| Составление смет по заказам | |
| Предварительная увязка сроков выполнения заказов | |
| Работа над договорами с заказчиками | |
| Проработка вопросов конструкторской подготовки по заказам | |
| Проработка вопросов технологической подготовки выполнения заказов | |
| Проработка вопросов материально-технического обеспечения заказов | |
| Уточнение смет затрат по заказам | |
| Заключение договоров с заказчиками | |
| Уточнение календарного графика работы над портфелем заказов | |
| Предварительная работа с потенциальными поставщиками (в том числе поиск потенциальных поставщиков) | |
| Формирование портфеля принятых заказов с учетом заключенных договоров | |
| Заключение договоров на поставку материальных ресурсов | |
| Построение цикловых графиков работы над основными элементами заказов | |
| Расчет длительностей циклов и опережений по каждому из принятых заказов | |
| Построение цикловых графиков выполнения заказов | |
| Разработка годовой программы выполнения заказов | |
| Формирование программы работ над заказами по коротким плановым периодам (распределение годовой программы по коротким плановым периодам – кварталам, месяцам) | |
| Формирование базы данных для оперативного управления выполнением заказов | |
| Оперативный учет хода выполнения заказов | |
| Продолжение таблицы 3.8. | |
| Увязка работ над заказами в конкретном коротком периоде и построение «Единого графика работ» | |
| Контроль и регулирование хода выполнения заказов | |
| Актуализация базы данных | |
| Оформление актов приемки-сдачи заказа | |
| Расчеты с заказчиками |
Поиск по сайту: