Однопродуктовая макроэкономическая модель оптимального развития экономики

, , (3.2.1)

где – капитал, – живой труд.

Эти ресурсы, как правило, наиболее существенные в производственном процессе, возможные остальные для простоты не учитываем.

Предположения (3.2.1), разумеется, справедливы в определенной области значений производственных факторов. Например, использование в фармацевтике и медицине малыми дозами некоторых ядов (наркотиков) в составе лекарств лечит человека, а большое – может привести к тяжелым заболеваниям вплоть до летального исхода; то же можно утверждать в отношении чрезмерного количества трудовых ресурсов, когда их излишек снижает эффективность производства, вно­ся в него беспорядок и неорганизованность. Тем не менее будем предполагать исключительными подобные случаи, считая условия (3.2.1) в разумных пределах нормальными для практики.

Представленным формулами (3.2.1) условиям отвечают мультипликативные, так называемые неоклассические ПФ вида

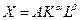, , , , (3.2.2)

где –валовой выпуск продукции;

– выпуск продукции при единичных затратах капитала и живо­го труда;

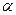и –эластичность выпуска продукции соответственно по капиталу и живому труду.

При 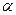>> производство называют капиталоемким, при 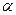<< – трудоемким.

При ПФ (3.2.2) называют ПФ Кобба-Дугласа.

Неоклассическая ПФ дает возможность отразить эффект масштаба производства, который проявляется только при одновременном измене­нии факторов и . Пусть эти факторы изменяются в раз. Тогда

. (3.2.3)

Различные значения определяют следующие режимы развития экономики:

Ö если 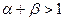- имеет место интенсивный способ развития, т. е. с ростом масштаба производства в раз выпуск продукции возрастает более чем в раз;

Ö если – производство неэффективное, т.е. выпуск продукции возрастает, но менее чем в раз;

Ö если (ПФ Кобба-Дугласа) – имеет место нормальное развитие экономики за счет интенсивных факторов производства [18].

Наблюдения показывают, что в условиях экстенсивного производства увеличение затрат только одного из факторов – приводит к снижению эффективности его использования, т. е.

, .

Такое явление называют эффектом насыщения. Оно означает, что каждая последующая единица возрастающего фактора соединяется с меньшим количеством другого фактора и его рост дает уменьшающийся прирост продукции. Например, при многостаночной организации производства значительное увеличение числа станков, приходящихся на одного рабочего в условиях неизменной технологии, квалификации работников и характеристик станков, уменьшают эффективность использо­вания оборудования. Примерно то же происходит и в случае, когда руководитель производственного коллектива большую часть работы берет на себя, а не делегирует, хотя бы частично, другим сотрудникам.

Он при этом все сам не успевает или делает плохо – его возможности по управлению достигли предела.

Для экстенсивного развития характерно:

, (3.2.5)

Это означает, что при отсутствии факторов или при их последующем приросте на бесконечно малую величину или скорость возрастания выпуска продукции становится бесконечно большой.

Наоборот, в случае чрезмерно большого возрастания факторов или

, (3.2.6)

прирост их эффективности снижается до нуля. Относительный прирост продукции возрастает в процентном отношении, что видно из следующего графика, отраженного на рисунке 3.1.

На рисунке 3.1. приведен график подобной функции в зависимости от аргумента при фиксированном значении другого аргумента .

Рисунок 3.1. Зависимость выпуска продукции от капитала

(при фиксированном значении живого труда )

Упомянутые выше коэффициенты эластичности ПФ по факторам и определяются как отношение предельной эффективности к средней:

, (3.2.7)

Рассмотренные ПФ имеют статический характер, в них в явном виде отсутствует показатель времени и не учитывается фактор научно-технического прогресса (НТП): производственные навыки, обусловленные длительностью моделируемого производственного процесса, образованность работников, общий уровень научно-технического раз­вития общества и т.д.

Простейший способ компенсации всех названных недостатков –автономный НТП, когда статическая ПФ умножается на эмпирически возрастающую функцию времени . В большинстве случаев , где – темп роста НТП. Преимущество такого спо­соба отражения в экономико-математических моделях динамики НТП – в его технической простоте (по существу не влияет на усложнение техники моделирования). Недостаток же – в сокрытии причин и качественных разновидностей НТП. Получается, что он возникает как бы из ничего, общество не затрачивает дополнительных ресурсов, что, очевидно, нереально.

В последующей части главы будут рассматриваться ПФ с учетом автономного НТП в виде

. (3.2.8)

На ограниченных отрезках времени (в основном до 5 лет) при статистически определенных значениях получаемые с использованием формулы (3.2.8) результаты оказываются удовлетворительными, по меньшей мере, на качественном уровне.

Оптимизационная модель макроэкономической динамики.

Магистральная теория.

В качестве практического применения достаточных условий оптимальности рассмотрим однопродуктовую экономи­ческую систему, непрерывную по времени, близкую к модели Солоу-Севана [34].

С формальной точки зрения данная модель представляет пример задачи, линейной по управлению, с ограничениями на управление. В содержательном же отношении это характерная модель экономической динамики.

Итак, пусть в экономической системе производится в единицу времени валовой продукт . В соответствии с уравнением межотраслевого баланса он разделяется на две части:

(3.2.9)

где –часть валового продукта, необходимая для производства (например, используется в качестве сырья или полуфабрикатов для последующего производства);

0< <1 – коэффициент прямых затрат;

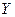–конечный продукт, используемый в непроизводственной сфере: для обеспечения жизнедеятельности общества, создания запасов и резервов, обороны, внешней торговли, в инвестированной деятельности и др.

В структуре конечного продукта выделим две важнейшие составляющие:

(3.2.10)

где – часть конечного продукта, идущая на непроизводственное текущее потребление;

– часть, идущая на инвестиции.

В формуле (3.2.10) можно выделить и другие составляющие, например, инвестиции, идущие на развитие науки и техники, что, в свою очередь, влияет на развитие научно-технического прогресса (так называемого, овеществленного). Однако, последнее не является структурной составляющей создаваемой модели, и мы ограничиваемся формулой (3.2.10).

Обозначим через – количество основных производственных фондов (капитал) в системе в момент . Будем считать, что прирост капитала в единицу времени равен количеству инвестиций в момент минус их часть, идущую на амортизацию (восстановление или ремонт уже имеющихся основных производственных фондов)

(3.2.11)

где – коэффициент амортизации, заданное число.

Допустим, как уже отмечалось в п. 3.2.1, задана отвечающая автономному НТН производственная функция

, (3.2.12)

где – количество трудовых ресурсов в момент .

Таким образом, в соответствии с формулами (3.2.9) – (3.2.12) получаем:

откуда

или

(3.2.13)

Формула (3.2.13) представляет уравнение процесса. В ней – внешний фактор, количество трудовых ресурсов, которое будем считать заданным; – состояние, – управление.

Таким образом, сущность управления отвечает принимаемому в момент решению, какую часть конечного продукта 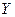следует направить на текущее потребление и, соответственно, сколько на инвестиции.

Поскольку речь идет об оптимальном выборе, продолжим формирование оптимизационной модели.

Поскольку, с одной стороны, , а с другой то имеем ограничения на управление

(3.2.14)

Будем считать, что , где – темп роста народонаселения. В течение рассматриваемого периода времени будем предполагать .

Функция имеет вид

, (3.2.15)

В этом случае, согласно п.3.2.1, имеем дело с ПФ Кобба-Дугласа с учетом автономного научно-технического прогресса, что соответствует нормальному развитию экономики.

В результате всех проведенных выкладок имеем

или

, (3.2.16)

где .

Пусть заданы начальное и конечное условия:

. (3.2.17)

Таким образом, объединяя в совокупность все приведенные выше формулы (5.14), ограничение на состояние , (3.2.15), (3.2.16), (3.2.17) получаем:

а) уравнение процесса:

б) ограничение на состояние:

в) ограничение на управление:

г) граничные условия:

.

При ограничениях а) – г) в качестве критерия оптимальности управления зададим максимизацию дисконтированного средневзвешенного душевого потребления в течение планового периода :

д)

где – коэффициент дисконтирования. Он указывает, что с возрастанием величины степень важности потребления благ уменьшается с точки зрения планирования в настоящий момент.

Теперь в виде соотношений а) – д) задача поставлена полностью. Чтобы иметь возможность в дальнейшем сопоставлять уровни экономического развития больших и малых стран, перейдем в поставленной задаче к показателям на душу населения. Введем обозначения:

– фондовооруженность на одного работающего;

– среднедушевое потребление.

Итак,

; ; .

Соответственно, ограничения а) – г) и функционал д) преобразуется следующим образом:

а) – уравнение процесса;

б) ограничение на состояние:

в) ограничение на управление:

г) граничные условия:

д) функционал:

Условия а) – д) представляют задачу, линейную относительно управления с, с ограничениями на управление в).

Для построения «усов» необходимо решить уравнение процесса а) для вариантов

и .

В случае получаем нелинейное дифференциальное уравнение Бернулли:

. (3.2.18)

Его линеаризация осуществляется посредством следующей постановки:

. (3.2.19)

Выражения (3.2.19) подставляем в уравнение (3.2.18) и после сокращения на получаем относительно 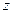линейное неоднородное дифференциальное уравнение первого порядка:

. (3.2.20)

Общее решение неоднородного уравнения (3.2.20) состоит из суммы общего решения однородного уравнения и частного решения неоднородного уравнения :

. (3.2.21)

Для нахождения общего решения однородного уравнения составляем характеристическое уравнение:

, (3.2.22)

откуда

и соответственно

. (3.2.23)

где – произвольная постоянная интегрирования.

В соответствии с видом правой части уравнения (3.2.20) частное решение неоднородного уравнения ищем виде

(3.2.24)

где – искомая величина, подлежащая определению.

Подставляем выражение (3.2.24) в уравнение (3.2.20), сокращаем слагаемые в левой и в правой частях на 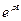и получаем:

. (3.2.25)

Используя формулы (3.2.21), (3.2.23), (3.2.24) и (3.2.25),получаем общее решение неоднородного уравнения:

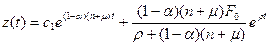. (3.2.26)

Согласно (3.2.19) и (3.2.26) формула для фондовооруженности имеет вид:

. (3.2.27)

Обратим внимание, что при (асимптотическое поведение) при любом значении первое слагаемое в (3.2.27)стремится к нулю, а второе – к бесконечности. Из начального условия определяем и тем самым получаем уравнение кривой . Заметим, что аналитическое вычисление произвольной постоянной интегрирования вряд ли возможно, но численным методом можно рассчитать с приемлемой

точностью.

Аналогичным образом определяется из конечного условия
и тем самым получаем уравнение «уса» .

Для построения «усов» и подставим в уравнение
процесса

а)

и получим дифференциальное уравнение с разделяющимися переменными

. (3.2.28)

Его общее решение

. (3.2.29)

Значение произвольной постоянной вычислим два раза, исходя из условий

и ,

при этом определяется по формуле (3.2.29).

В конечном итоге будем иметь:

; . (3.2.30)

В результате получим допустимую область значений (рисунок 3.2).

Теперь перейдем к построению функции .

Согласно условиям задачи а) – д) настоящего параграфа имеем:

;

; .

Отсюда согласно получаем:

. (3.2.31)

Рисунок 3.2. Допустимая область значений фондовооруженности (находится внутри отштрихованных значений _, ; ).

Максимизация функции осуществляется по при фиксированном значении . Поэтому множитель при фиксированном значении можно опустить и рассматривать функцию

. (3.2.32)

Формула (5.32) состоит из двух слагаемых:

линейной части

и нелинейной

Их графики и сумма показаны на рисунке 3.3.

Рисунок 3.3. Графики функций , , , .

В точке : в ней достигается единственный безусловный максимум функции .

Проведем соответствующие вычисления:

отсюда , где 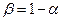. (3.2.33)

Определенную по формуле (3.2.33) функцию называют уравнением магистрали.

Магистраль – это такая зависимость , по которой шло бы развитие фондовооруженности при отсутствии ограничений на душевое потребление. Согласно приведенному ранее функция играет роль управления.

Магистраль представляет собой равномерный рост фондовооруженности с темпом 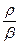. В частности, если НТП отсутствует, т.е. , .

Определим, чему равно на магистрали управление (душевое потребление). Из уравнения процесса а) имеем:

. (3.2.34)

Подставляя в (3.2.34) вместо значение (3.2.33), получаем:

(3.2.35)

Как видно из (3.2.35), на магистрали относительное душевое потребление растет с тем же темпом 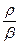, что и фондовооруженность. В случае (нет НТП) душевое потребление на магистрали с = const.

Зная магистраль, легко находим оптимальное решение: там, где магистраль лежит внутри заштрихованной области на рисунке 3.2, она является и оптимальным решением. Если она лежит вне заштрихованной области, на этих участках оптимальное решение проходит по ближайшей к магистрали границе. На рисунке 3.4 оптимальное решение показано жирной линией.

Аналитический вид функции задается формулой (3.2.36):

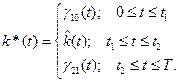. (3.2.36)

Рисунок 3.4. Оптимальное значение фондовооруженности .

Соответственно функция оптимального душевого потребления имеет вид

. (3.2.37)

Если магистраль проходит выше начального условия и ниже конечного , а именно этот случай содержательно наиболее интересен, то оптимальный режим управления экономикой заключается в следующем: сначала максимально развиваются производственные фонды (капитал), а потребление равно нулю, форсированно доходим до магистрали в момент _. Далее до момента развитие идет по магистрали: с постоянным темпом (формула (3.2.34)) растут потребление и фондовооруженность. При ≤ t ≤ весь конечный продукт может тратиться на потребление. Читателю предлагается самостоятельно рассмотреть случаи > и > .

Глядя на рисунок 3.4, можно представить такую образную картину сути магистрали и магистрального функционирования экономики. Допустим, что мы находимся в начальном пункте и нам нужно на автомобиле переехать в конечный пункт . Неподалеку от проходит автотрасса – аналог в данном случае магистрали. Мы оптимальным образом от по местной дороге доезжаем до автотрассы, далее в момент выезжаем на магистраль и едем по ней до момента , после чего съезжаем с магистрали и по местной дороге – добираемся до конечного пункта . Эта интерпретация дает интуитивное представление об оптимальном развитии экономики.

Экспериментальные расчеты по оценке оптимального развития США за период 22 года (1947 – 1968) на примерах внутренней частной и несельскохозяйственной экономики были проведены согласно изложенной методике и отражены в [18].

Сравнение с реальным развитием экономики США за этот период, конечно, не отвечает адекватному совпадению результатов, но на качественном уровне их можно считать приемлемыми. Различие примерно в 2 раза: расчетные данные более оптимистичные, чем фактические. Оно объясняется, по-видимому, не вполне точным совпадением фактических и расчетных исходных данных по фигурирующим в модели показателям, прежде всего качественной оценкой производственных функций и средствами описания НТП.

Поиск по сайту: