Система Коши-Римана

Система линейных однородных дифференциальных уравнений первого порядка в частных производных с двумя независимыми переменными x и y

(4.1.1)

называется системой Коши-Римана. Это система эллиптического типа.

Напомним, что система дифференциальных уравнений, матричная запись которой имеет вид

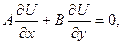
где

U=

относится к эллиптическому типу, если квадратичная форма

положительно (или отрицательно) определена.

Поскольку в случае системы (4.1.1) имеем:

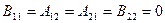
и квадратичная форма

оказывается положительно определенной, система Коши-Римана является системой эллиптического типа.

Если - произвольная гармоническая функция, т.е. если она удовлетворяет уравнению Лапласа

то пара функций является решением системы Коши-Римана, что несложно проверить непосредственной подстановкой:

Последнее равенство имеет место в силу известной из математического анализа теоремы о непрерывных смешанных производных. Ниже будет показано, что действительная и мнимая части 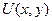и функции 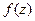, аналитической в некоторой области, обладают дифференцируемыми (следовательно, и непрерывными) частными производными любого порядка. Из непрерывности функций и следует непрерывность функций и , а непрерывные смешанные производные и всегда равны.

Поиск по сайту: