Использование сетевых моделей в управленческих решениях

Основные понятия и определения сетевого графа, правила построения

Сетевой граф представляет собой сочетание вершин и дуг. В графе, построенном в терминах работ, вершинами являются события, а дугами – работы.

Основными элементами сетевой модели являются: событие, работа, продолжительность работы; величина ресурса, потребного для выполнения каждой из работ; различные пути достижения конечной цели, критический путь.

Событие – это результат выполнения всех входящих в него работ, при этом допускается, что событие наступает мгновенно после выполнения всех входящих в него работ, поэтому продолжительность свершения события равна нулю. Событие обозначается кружком .

При нумерации событий его номер проставляется внутри кружка .

В любом сетевом графе есть два особых события: исходное и завершающее. Исходное событие не имеет входящих в него работ и обозначается как начальное. Это отправной момент начала работ по данному сетевому графу. В завершающем событии работы только сходятся, но ни одна работа из него не выходит.

Событие, из которого выходит работа, называется начальным; а событие, в которое входит эта работа, – конечным:

где 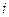– начальное событие, ;

– конечное событие, ;

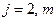– работа.

События 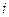и называют смежными событиями.

В сетевом графе различают несколько видов работ:

· действительная работа;

· ожидание;

· фиктивная работа (зависимость).

Под действительной работой понимается процесс, требующий затрат времени и ресурсов. Каждая работа характеризуется либо затратами труда, либо стоимостью ее выполнения. Кроме того, выполнение работы связано с необходимостью использования различных ресурсов, поэтому в числе характеристик каждой из работ выступает также показатель количества источников ресурса (ресурсов), необходимых для выполнения конкретной работы. Для выполнения работы может потребоваться один или несколько видов ресурсов. Количество требующихся ресурсов определяет сетевую модель как одноресурсную или многоресурсную. Действительная работа на сетевом графе отображается сплошной стрелкой .

Например, необходимо произвести сборку станка, которая включает выполнение комплекса работ (технологических операций). Выполнение этих операций требует: привлечения рабочих (слесарей-сборщиков); подготовки площадки для выполнения операций сборки; специальных сборочных приспособлений; необходимого для сборки комплекта деталей, узлов и т.п., то есть трех источников ресурсов – живого труда, средств и предмета труда. Потребность в каждом из этих ресурсов определяется сложностью собираемого станка, особенностями выполнения операций сборки и т.д.

Все эти подготовительные и технологические операции сборки требуют соответствующих видов ресурсов, характеризуются определенной продолжительностью выполнения, следовательно, являются действительными работами. Эти работы взаимоувязаны между собой и, таким образом, могут быть представлены в виде сетевого графа.

Ожидание – это процесс, который требует только затрат времени и не нуждается в использовании ресурсов (например, процесс остывания детали после термообработки, затвердевание бетона, и др.). Ожидание на графе также изображается сплошной линией .

«Фиктивная работа», или зависимость, отражает логическую связь между двумя или несколькими событиями. «Фиктивная работа» не требует для своего осуществления ни затрат времени, ни ресурсов. Этот вид работы указывает только на то, что определенное событие не может наступить, а работа не может начаться без наступления другого события или выполнения другой работы.

Например, необходимо определить потребность организации в материальных ресурсах. Для такого расчета требуются производственная программа в разрезе выпускаемых наименований изделий и нормы расхода конкретного материала на то или иное наименование изделия. Производственную программу формирует производственно-диспетчерский отдел, норму расхода материала устанавливает технологический отдел. Расчет потребности в материалах не может быть начат без получения соответствующей информации от указанных отделов организации, т.е. без завершения работ по указанным ранее расчетам. Таким образом, между расчетом потребности в материалах и формированием производственной программы и установлением норм расхода материалов существует зависимость – фиктивная работа. Фиктивная работа на сетевом графе отображается пунктирной линией .

Работа, непосредственно предшествующая данной, называется непосредственно предшествующей работой; а непосредственно следующая за данной – непосредственно следующей.

Работы (действительные, ожиданий и фиктивные), выходящие из начального события, не имеют работ непосредственного предшествования; а работы, входящие в конечное событие, не имеют работ непосредственного следования. Остальные работы могут иметь одну или несколько непосредственно предшествующих и непосредственно следующих работ.

Важным элементом сетевого графа является путь – непрерывная последовательность работ от начального или какого-либо промежуточного события до конечного. Путь определяется по направлению стрелок, причем ни один путь не должен дважды проходить через одно и то же событие. Длина пути рассчитывается как сумма продолжительностей составляющих его работ. Продолжительность выполнения отдельных работ устанавливается различными методами: расчетно-аналитическим, аналогов, экспертным, статистическими методами, например, методом средних оценок и т.д. Трудоемкость выполнения работ на графе проставляется над стрелкой, которая обозначает данную работу. Различают различные виды путей: предшествующий событию, полный и критический.

Предшествующий путь – это путь от начального до данного события;

· полный – от начального до конечного события;

· критический – наименьший по продолжительности из всех полных путей, за время прохождения которого будут выполнены все без исключения работы сетевого графа, и наступят все события.

При построении сетевых графов необходимо соблюдать определенные правила:

1. Сетевой граф может иметь только одно начальное и только одно конечное событие.

2. Между двумя смежными событиями сетевого графа может проходить только одна работа. Если два смежных события связаны несколькими работами, тогда эти работы должны быть объединены либо в одну, либо «разведены» через дополнительно введенное событие (рисунок 3.8).

3.

а) б)

Рисунок 3.8. а) неправильно; б) правильно

3. Если событие служит началом нескольких работ, которым непосредственно предшествуют различные работы, то на графе вводится фиктивная работа и дополнительное событие.

4. В сетевом графе не должно возникать «тупиковых» ситуаций, т.е. не должно быть событий, кроме конечного, из которых не выходит ни одной работы (рисунок 3.9). Работа, входящая в такое событие, должна быть присоединена к конечному событию (рисунок 3.9).

а) б)

Рисунок 3.9. а) неправильно; б) правильно

5. В сетевом графе не должно быть событий, кроме начального, в которые не входит ни одной работы. Такие события получили название «хвостовых» (рисунок 3.10). При наличии такой ситуации работа, исходящая из этого события, должна быть присоединена к начальному событию.

а) б)

Рисунок 3.10. а) неправильно; б) правильно

6. В сетевом графе не должно быть замкнутых контуров, т.е. последовательности работ, приводящей к событию, из которого они вышли (рисунок 3.11).

Рисунок 3.11. Неправильное построение

7. На сетевом графе не должно быть излишних логических связей и событий.

8. Форма представления сетевого графа должна быть простой, исключающей или минимизирующей число пересекающихся работ.

9. При построении сетевого графа необходимо строго соблюдать технологическую последовательность выполнения работ для достижения поставленной цели.

10. События сетевого графа нумеруются арабскими цифрами, путем последовательного перебора событий; а при наличии альтернатив – слева направо, сверху вниз, приоритетность при этом отдается событию, в которое входит работа, исходящая из события с наименьшим номером.

11. Любую работу сетевого графа можно зашифровать: буквами алфавита (русского, латинского, греческого и т.п.); номерами натурального ряда чисел или, используя номера событий, соединяемых данной работой.

При использовании алфавита или натурального ряда чисел для кодирования работ взаимосвязи и взаимозависимости работ сетевого графа устанавливаются путем указания для каждой работы соответственно шифра работы (работ) непосредственного предшествования. Если для этой цели использовать номера событий, то каждой работе можно присвоить два номера: первый – номер события, из которого данная работа выходит; второй – в которое работа входит. Например, работа, выходящая из события 5 и входящая в событие 7, будет иметь шифр 5-7.

На сетевом графе не должно быть нескольких работ с одинаковым шифром.

После построения сетевого графа его события нумеруются (кодируется), при этом может использоваться натуральный ряд чисел, начиная с 1.

В качестве одного из возможных вариантов решения можно воспользоваться методом вычеркивания дуг. Последовательность его реализации следующая (рисунок 3.12):

1. На сетевом графе отыскивается начальное событие, т.е. событие, не имеющее непосредственно предшествующих работ. Событию присваивается первый номер (рисунок 3.12, а).

2. На графе условно вычеркиваются все работы, выходящие из этого события; таких работ может быть одна или несколько (рисунок 3.12 б, в).

3. Выбирается событие, в которое входят все «вычеркнутые» работы. Таких событий может быть одно или несколько. Если событие одно (рисунок 3.12 в), то ему присваивается очередной номер натурального ряда чисел (рисунок 3.12 в), и последующие процедуры кодирования осуществляются, начиная с пункта 2.

а) б) в)

г) д) е)

ж) з)

и) к)

Рисунок 3.12. Кодирование событий и работ сетевого графа методом вычеркивания дуг

Если таких событий несколько (альтернативные события – рисунок 3.12 в, г, д), то их кодирование осуществляется с соблюдением следующего правила: альтернативные события сетевого графа нумеруются слева направо, т.е. от начального события к конечному, и сверху вниз, т.е. в соответствии с графическим отображением этих альтернативных событий, при этом приоритет отдается работе, номер начального события которой меньше. Для нумерации событий используются свободные очередные номера натурального ряда чисел. Нумерация альтернативных событий осуществляется последовательным перебором каждого из этих событий. После присвоения очередного номера одному из альтернативных событий, выбранных по изложенному выше правилу (рисунок 3.12 в, г, д, и), процедура кодирования продолжается, начиная с пункта 2.

4. Операции кодирования повторяются до выхода на конечное событие сетевого графа (рисунок 3.12 к).

Поиск по сайту: