Многоканальная СМО с неограниченной очередью (М/М/n)

Для рассмотрения этой СМО снова применим уже использованный нами алгоритм рассмотрения:

1. Зададим множество состояний:

S0 – система пуста;

S1 – один канал занят;

S2 – два канала заняты;

Sn – n каналов заняты;

Sn+k – n каналов заняты, k заявок в очереди..

2. Составим граф состояний и разметим его.

3. По формулам гибели и размножения найдем финальные вероятности.

Финальные вероятности существуют если

…

…

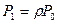
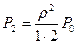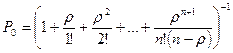
4. Характеристики эффективности.

Среднее число занятых каналов:

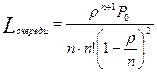
По формуле Литтла:

Пример. В порту имеется два причала для разгрузки грузовых судов. Интенсивность потока судов равна 0,8 судов в сутки. Среднее время разгрузки одного судна составляет 2 сут. Предполагается, что очередь ожидающих разгрузки судов может быть неограниченной длины.

Найти среднее время пребывания судна в порту.

Имеем: m=2, l=0,8 сут^-1, , .

Находим:

;

;

.

Итак, сут.

Частным случаем рассмотренной нами системы является СМО, в которой очередь не бесконечна, а имеет конечное значение. Этот случай рассматривается ниже

СМО с ограниченной длиной очереди.

СМО с ограниченной длиной очереди является такая система, в которой требование, поступающее на обслуживание, покидает систему, если заняты все каналы обслуживания, и в накопителе заняты все места.

Вероятности состояний S₀, S₁,…, S_N находят по формуле

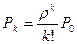, где .

Вероятности состояний определяют с помощью формулы

, где , l – максимальная длина очереди.

Вероятность P₀ подсчитывают по формуле .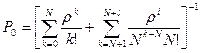

В большинстве практических задач должно соблюдаться отношение , тогда выражение для P₀ можно переписать в следующем виде

.

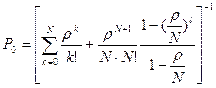Вероятность отказа в обслуживании определяется из выражения

.

Среднее число каналов, занятых в обслуживании, и коэффициент занятости определяются:

; .

Среднее число свободных аппаратов и коэффициент простоя определяются:

; .

Средняя длина очереди определяется с помощью выражения:

.

Пример. На автозаправочной станции установлены три колонки для выдачи бензина. Около станции находится площадка на три машины для их ожидания в очереди. На станцию прибывает в среднем две машины в минуту. Среднее время заправки одной машины 1мин. Требуется определить вероятность отказа и среднюю длину очереди.

Имеем: N=3, l=3, l=2мин^-1, =1мин, . Находим: , , тогда

,

,

.

Таким образом, , машины.

Поиск по сайту: