 |
јвтојвтоматизаци€јрхитектурајстрономи€јудитЅиологи€Ѕухгалтер般оенное дело√енетика√еографи€√еологи€√осударствоƒомƒругое∆урналистика и —ћ»»зобретательство»ностранные €зыки»нформатика»скусство»стори€ омпьютеры улинари€ ультураЋексикологи€ЋитератураЋогикаћаркетингћатематикаћашиностроениећедицинаћенеджментћеталлы и —варкаћеханикаћузыкаЌаселениеќбразованиеќхрана безопасности жизниќхрана “рудаѕедагогикаѕолитикаѕравоѕриборостроениеѕрограммированиеѕроизводствоѕромышленностьѕсихологи€–адио–егили€—в€зь—оциологи€—порт—тандартизаци€—троительство“ехнологии“оргов눓уризм‘изика‘изиолог舑илософ舑инансы’ими€’оз€йство÷еннообразование„ерчениеЁкологи€ЁконометрикаЁкономикаЁлектроникаёриспунденкци€
√рафическое изображение статистических данных
—татистическое распределение изображаетс€ графически с помощью полигона и гистограммы.
ќпределение. ѕолигоном частот называют ломаную, отрезки которой соедин€ют точки с координатами  ; полигоном частостей Ц с координатами
; полигоном частостей Ц с координатами  , где
, где  ,
,  .
.
ѕолигон служит дл€ изображени€ дискретного статистического р€да.
ѕолигон частостей €вл€етс€ аналогом многоугольника распределени€ дискретной случайной величины в теории веро€тностей.
ќпределение. √истограммой частот (частостей) называют ступенчатую фигуру, состо€щую из пр€моугольников, основани€ которых расположены на оси  и длины их равны длинам частичных интервалов
и длины их равны длинам частичных интервалов  , а высоты равны отношению:
, а высоты равны отношению:
 - дл€ гистограммы частот;
- дл€ гистограммы частот;  - дл€ гистограммы частостей.
- дл€ гистограммы частостей.
√истограмма €вл€етс€ графическим изображением интервального р€да.
ѕлощадь гистограммы частот равна  , а гистограммы частостей равна 1.
, а гистограммы частостей равна 1.
ћожно построить полигон дл€ интервального р€да, если его преобразовать в дискретный р€д. ¬ этом случае интервалы замен€ют их серединными значени€ми и став€т в соответствие интервальные частоты (частости). ѕолигон получим, соединив отрезками середины верхних оснований пр€моугольников гистограммы.
ѕример 3. ƒана выборка значений случайной величины  объема 20:
объема 20:
12, 14, 19, 15, 14, 18, 13, 16, 17, 12
18, 17, 15, 13, 17, 14, 14, 13, 14, 16
“ребуетс€: - построить дискретный вариационный р€д;
- найти размах варьировани€  , моду
, моду  , медиану
, медиану  ;
;
- построить полигон частостей.
¶ 1)–анжируем выборку: 12, 12, 13, 13, 13, 14, 14, 14, 14, 14,
15, 15, 16, 16, 17, 17, 17, 18, 18, 19.
2) Ќаходим частоты вариантов и строим дискретный вариационный р€д (табл.3)
“аблица 3.
«начени€ вариантов 
| |||||||||
„астоты 
| 
| ||||||||
„астости 
| 
| 
| 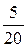
| 
| 
| 
| 
| 
| 
|
3) ѕо результатам таблицы 3 находим:
 ,
,  ,
, 
4)—троим полигон частостей.

–ис. 2 Ш
ѕример 4. –езультаты измерений отклонений от нормы диаметров
50 подшипников дали численные значени€ (в мкм), приведенные в табл. 4.
“аблица 4.
| -1,760 | -0,291 | -0,110 | -0,450 | 0,512 |
| -0,158 | 1,701 | 0,634 | 0,720 | 0,490 |
| 1,531 | -0,433 | 1,409 | 1,740 | -0,266 |
| -0,058 | 0,248 | -0,095 | -1,488 | -0,361 |
| 0,415 | -1,382 | 0,129 | -0,361 | -0,087 |
| -0,329 | 0,086 | 0,130 | -0,244 | -0,882 |
| 0,318 | -1,087 | 0,899 | 1,028 | -1,304 |
| 0,349 | -0,293 | 0,105 | -0,056 | 0,757 |
| -0,059 | -0,539 | -0,078 | 0,229 | 0,194 |
| 0,123 | 0,318 | 0,367 | -0,992 | 0,529 |
ƒл€ данной выборки: - построить интервальный вариационный р€д;
- построить гистограмму и полигон частостей.
¶ 1. —троим интервальный р€д.
ѕо данным таблицы 4 определ€ем: 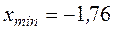 ;
; 
ƒл€ определени€ длины интервала 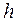 используем формулу —терджеса:
используем формулу —терджеса:
 .
.
„исло интервалов  .
.

ѕримем 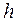 =0,6,
=0,6,  .
.
«а начало первого интервала примем величину
 .
.
онец последнего интервала должен удовлетвор€ть условию:
 .
.
ƒействительно, 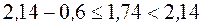 ;
;  .
.
—троим интервальный р€д (табл. 5).
“аблица 5.
| »нтервалы | 
| 
| 
| 
|
| ѕодсчет частот | 
| 
| 
| 
|
„астоты 
| ||||
„астости 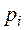
| 
| 
| 
| 
|
| »нтервалы | 
| 
| 
| |
| ѕодсчет частот | 
| 
| 
| |
„астоты 
|  ; ;
| |||
„астости 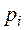
| 
| 
| 
|  . .
|
—троим гистограмму частостей.

–ис.3
¬ершинами полигона €вл€ютс€ середины верхних оснований пр€моугольников гистограммы.
”бедимс€, что площадь гистограммы равна 1.

 Ш
Ш
ѕоиск по сайту: