 |
јвтојвтоматизаци€јрхитектурајстрономи€јудитЅиологи€Ѕухгалтер般оенное дело√енетика√еографи€√еологи€√осударствоƒомƒругое∆урналистика и —ћ»»зобретательство»ностранные €зыки»нформатика»скусство»стори€ омпьютеры улинари€ ультураЋексикологи€ЋитератураЋогикаћаркетингћатематикаћашиностроениећедицинаћенеджментћеталлы и —варкаћеханикаћузыкаЌаселениеќбразованиеќхрана безопасности жизниќхрана “рудаѕедагогикаѕолитикаѕравоѕриборостроениеѕрограммированиеѕроизводствоѕромышленностьѕсихологи€–адио–егили€—в€зь—оциологи€—порт—тандартизаци€—троительство“ехнологии“оргов눓уризм‘изика‘изиолог舑илософ舑инансы’ими€’оз€йство÷еннообразование„ерчениеЁкологи€ЁконометрикаЁкономикаЁлектроникаёриспунденкци€
ћатематического ожидани€ при неизвестной дисперсии
ѕусть случайна€ величина  имеет нормальное распределение:
имеет нормальное распределение:  , причем
, причем  - неизвестно,
- неизвестно,  - задана.
- задана.
≈сли  неизвестна, то пользуютс€ оценкой
неизвестна, то пользуютс€ оценкой  .
.
¬ведем случайную величину  ,
,
где  - исправленное среднее квадратическое отклонение случайной величины
- исправленное среднее квадратическое отклонение случайной величины  , вычисленное по выборке:
, вычисленное по выборке:
 ;
;
—лучайна€ величина 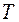 имеет распределение —тьюдента с
имеет распределение —тьюдента с  степенью свободы.
степенью свободы.
“огда доверительный интервал дл€ оценки  имеет вид:
имеет вид:
 ,
,
где 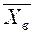 - выборочное среднее;
- выборочное среднее;
 - исправленное среднее квадратическое отклонение;
- исправленное среднее квадратическое отклонение;
 - находим по таблице квантилей распределени€ —тьюдента (ѕриложение 4) в зависимости от числа степеней свободы и доверительной веро€тности
- находим по таблице квантилей распределени€ —тьюдента (ѕриложение 4) в зависимости от числа степеней свободы и доверительной веро€тности  .
.
ѕример 7. ѕроизведено п€ть независимых наблюдений над случайной величиной  . –езультаты наблюдений таковы:
. –езультаты наблюдений таковы:
 ,
,  ,
,  ,
,  ,
,  .
.
ѕостроить дл€ неизвестного  доверительный интервал, если
доверительный интервал, если  .
.
¶ 1. Ќаходим  :
: 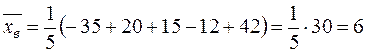
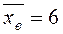
2. Ќаходим  :
:

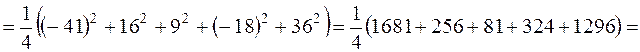
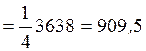
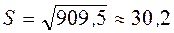
3. ѕо таблице квантилей распределени€ —тьюдента (ѕриложение 4) дл€  и
и  находим
находим  :
:
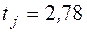
ƒоверительный интервал:
 или
или  . Ш
. Ш
ѕоиск по сайту: