 |
јвтојвтоматизаци€јрхитектурајстрономи€јудитЅиологи€Ѕухгалтер般оенное дело√енетика√еографи€√еологи€√осударствоƒомƒругое∆урналистика и —ћ»»зобретательство»ностранные €зыки»нформатика»скусство»стори€ омпьютеры улинари€ ультураЋексикологи€ЋитератураЋогикаћаркетингћатематикаћашиностроениећедицинаћенеджментћеталлы и —варкаћеханикаћузыкаЌаселениеќбразованиеќхрана безопасности жизниќхрана “рудаѕедагогикаѕолитикаѕравоѕриборостроениеѕрограммированиеѕроизводствоѕромышленностьѕсихологи€–адио–егили€—в€зь—оциологи€—порт—тандартизаци€—троительство“ехнологии“оргов눓уризм‘изика‘изиолог舑илософ舑инансы’ими€’оз€йство÷еннообразование„ерчениеЁкологи€ЁконометрикаЁкономикаЁлектроникаёриспунденкци€
ѕравило проверки
1. ¬ычисл€ем  и
и  (см. ѕример 5).
(см. ѕример 5).
2. Ќаходим теоретические частоты  .
.
»х можно вычислить двум€ способами.
ѕервый способ
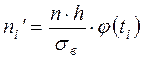 ,
,
где  - объем выборки,
- объем выборки, 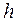 - шаг,
- шаг,  ;
;
 - функци€ √аусса, значение которой в точке
- функци€ √аусса, значение которой в точке 
находим по таблице (ѕриложение 1).
 - веро€тность попадани€ значений случайной
- веро€тность попадани€ значений случайной
величины  в
в  - й интервал.
- й интервал.
ƒл€ вычислени€  составл€ем табл. 9.
составл€ем табл. 9.
“аблица 9

| 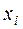
| 
| 
| 
| 
| 
| 
|

| 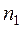
| 
| 
| 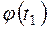
| 
| 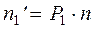
| |

| 
| 
| 
| 
| 
| 
| 
|
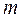
| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
|
¬торой способ.

где  - объем выборки,
- объем выборки,  ,
,
 - веро€тность попадани€
- веро€тность попадани€  в
в  - й интервал,
- й интервал,
 - значение функции Ћапласа (ѕриложение 2).
- значение функции Ћапласа (ѕриложение 2).
ѕолагают  ,
,  .
.
ƒл€ вычислени€  составл€ем табл. 10.
составл€ем табл. 10.
“аблица 10

| √раницы интервала | 
| √раницы интервала | 
| 
| 
| 
| ||
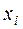
| 
| 
| 
| ||||||

| 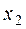
| 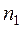
| 
| 
| -0,5 | 
| 
| 
| |

| 
| 
| 
| 
| 
| 
| 
| 
| 
|
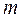
| 
| 
| 
| 
| 
| 
| 0,5 | 
| 
|

| 
| 
|
3. —равниваем эмпирические ( ) и теоретические (
) и теоретические ( ) частоты с помощью критери€ ѕирсона.
) частоты с помощью критери€ ѕирсона.
ƒл€ этого:
1) составл€ем расчетную табл.11, по которой находим
 - наблюдаемое значение критери€
- наблюдаемое значение критери€ 
“аблица 11.

| 
| 
| 
| 
|  
| 
| 
|
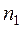
| 
| 
| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
| 
| 
|
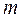
| 
| 
| 
| 
| 
| 
| 
|

| 
| 
|
онтроль:  .
.
2) Ќаходим число степеней свободы  :
: 
где 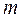 - число интервалов;
- число интервалов;  - число параметров предполагаемого распределени€,
- число параметров предполагаемого распределени€,
ƒл€ нормального распределени€ 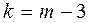 , так как
, так как  (нормальный закон распределени€ характеризуетс€ двум€ параметрами
(нормальный закон распределени€ характеризуетс€ двум€ параметрами  и
и  ).
).
4. ¬ таблице критических точек (квантилей) распределени€ 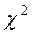
(ѕриложение 3) по заданному уровню значимости  и числу степеней свободы
и числу степеней свободы
находим  правосторонней критической области.
правосторонней критической области.
≈сли  - нет оснований отвергнуть гипотезу
- нет оснований отвергнуть гипотезу 
о нормальном распределении генеральной совокупности.
≈сли  - гипотезу отвергаем.
- гипотезу отвергаем.
«амечание.
1) ќбъем выборки должен быть достаточно велик  .
.
2) ћалочисленные частоты  следует объединить. ¬ этом случае и соответствующие им теоретические частоты также надо сложить.
следует объединить. ¬ этом случае и соответствующие им теоретические частоты также надо сложить.
≈сли производилось объединение частот, то при определении числа степеней свободы по формуле 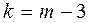 следует в качестве
следует в качестве 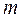 прин€ть число интервалов, оставшихс€ после объединени€ частот.
прин€ть число интервалов, оставшихс€ после объединени€ частот.
ѕример 10. ѕусть из генеральной совокупности  задана выборка объемом 50 (табл.4). “ребуетс€ проверить гипотезу
задана выборка объемом 50 (табл.4). “ребуетс€ проверить гипотезу 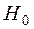 о нормальном распределении генеральной совокупности по данной выборке.
о нормальном распределении генеральной совокупности по данной выборке.
¶ 1. »з рассмотренных выше примеров известно:
- интервальный р€д табл. 12
“аблица 12
| »нтервалы | 
| 
| 
| 
|
„астоты 
|
| »нтервалы | 
| 
| 
| |
„астоты 
|  . .
|
- числовые характеристики выборки 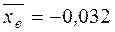 ,
,  ,
,
 ,
,  (см. ѕример 5).
(см. ѕример 5).
2. ѕроверим гипотезу 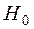 с помощью средних квадратических отклонений коэффициентов
с помощью средних квадратических отклонений коэффициентов  и
и  .
.
ритерием распределени€ выборки по нормальному закону €вл€етс€ равенство нулю коэффициентов  и
и  .
.
≈сли они отличны от нул€, то дл€ предварительного выбора закона распределени€ вычисл€ют средние квадратические отклонени€ дл€  и
и  :
:

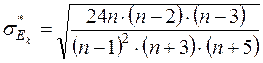
≈сли  и
и  отличаютс€ по модулю от нул€ не более чем на удвоенные средние квадратические отклонени€, то есть
отличаютс€ по модулю от нул€ не более чем на удвоенные средние квадратические отклонени€, то есть  и
и  , то можно предположить, что данна€ выборка распределена по нормальному закону.
, то можно предположить, что данна€ выборка распределена по нормальному закону.
–ассчитаем 
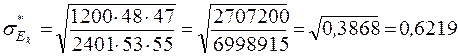 .
.
ƒл€  условие критери€ выполн€етс€:
условие критери€ выполн€етс€:  .
.
ƒл€  условие критери€ выполн€етс€:
условие критери€ выполн€етс€:  .
.
√ипотезу 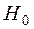 принимаем, то есть можно предположить, что генеральна€ совокупность
принимаем, то есть можно предположить, что генеральна€ совокупность  распределена по нормальному закону.
распределена по нормальному закону.
3. ѕроверим гипотезу 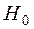 по критерию ѕирсона.
по критерию ѕирсона.
1) 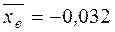 ,
,  .
.
2) Ќайдем теоретические частоты  вторым способом.
вторым способом.
»нтервальный р€д (табл.12) содержит интервалы с частотами меньшими 5. —ледовательно, два первых и два последних интервала объедин€ем, при этом соответствующие частоты суммируем.
—оставим расчетную табл.13 по форме табл.10.
“аблица 13

| √раницы интервала | 
| √раницы интервала | 
| 
| 
| 
| ||
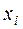
| 
| 
| 
| ||||||
| -2,06 | -0,86 | 
| -1,01 | -0,5 | -0,3438 | 0,1562 | 7,81 | ||
| -0,86 | -0,26 | -1,01 | -0,28 | -0,3438 | -0,1103 | 0,2335 | 11,675 | ||
| -0,26 | 0,34 | -0,28 | 0,45 | -0,1103 | 0,1736 | 0,2839 | 14,195 | ||
| 0,34 | 0,94 | 0,45 | 1,19 | 0,1736 | 0,3830 | 0,2094 | 10,47 | ||
| 0,94 | 2,14 | 1,19 | 
| 0,3830 | 0,5 | 0,1170 | 5,85 | ||

|
3) —равним эмпирические ( ) и теоретические (
) и теоретические ( ) частоты. ƒл€ этого составл€ем расчетную табл.14 по форме табл.11
) частоты. ƒл€ этого составл€ем расчетную табл.14 по форме табл.11
“аблица 14

| 
| 
| 
| 
|  
| 
| 
|
| 7,810 | 0,190 | 0,0361 | 0,0046 | 8,1946 | |||
| 11,675 | -0,675 | 0,4556 | 0,0390 | 10,3640 | |||
| 14,195 | 0,805 | 0,6480 | 0,0457 | 15,8507 | |||
| 10,470 | 0,530 | 0,2809 | 0,0268 | 11,5568 | |||
| 5,850 | -0,850 | 0,7225 | 0,1235 | 4,2735 | |||

| 0,2396 | 50,2396 |
онтроль: 
 . –асчеты проведены верно.
. –асчеты проведены верно.
4) «ададим  .
.
¬ычислим число степеней свободы  и найдем
и найдем  (ѕриложение 3). ѕолучим
(ѕриложение 3). ѕолучим  .
.
—ледовательно, нет оснований отвергать гипотезу 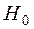 о нормальном распределении генеральной совокупности
о нормальном распределении генеральной совокупности  .
.
ƒругими словами различие между эмпирическими ( ) и теоретическими (
) и теоретическими ( ) частотами незначительное (случайное), которое можно объ€снить малым объемом выборки.
) частотами незначительное (случайное), которое можно объ€снить малым объемом выборки.
ѕостроим нормальную кривую. ƒл€ этого составим табл.15.
“аблица 15
| —ередины интервалов | -1,76 | -1,16 | -0,56 | 0,04 | 0,64 | 1,24 | 1,84 |

| 0,05 | 0,19 | 0,39 | 0,52 | 0,34 | 0,14 | 0,03 |
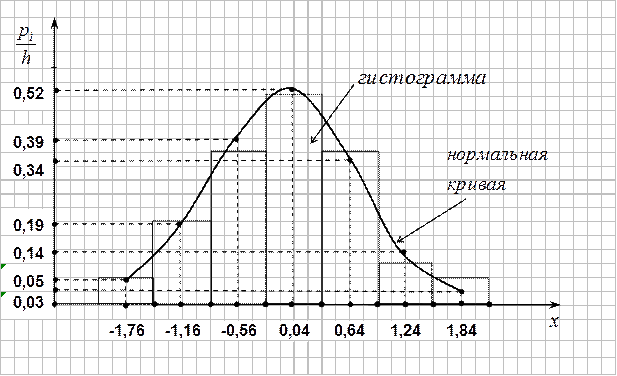
–ис.5
“ак как гипотеза о нормальном распределении не отвергаетс€, то нормальна€ крива€ хорошо сглаживает гистограмму. Ш
ѕоиск по сайту: