 |
јвтојвтоматизаци€јрхитектурајстрономи€јудитЅиологи€Ѕухгалтер般оенное дело√енетика√еографи€√еологи€√осударствоƒомƒругое∆урналистика и —ћ»»зобретательство»ностранные €зыки»нформатика»скусство»стори€ омпьютеры улинари€ ультураЋексикологи€ЋитератураЋогикаћаркетингћатематикаћашиностроениећедицинаћенеджментћеталлы и —варкаћеханикаћузыкаЌаселениеќбразованиеќхрана безопасности жизниќхрана “рудаѕедагогикаѕолитикаѕравоѕриборостроениеѕрограммированиеѕроизводствоѕромышленностьѕсихологи€–адио–егили€—в€зь—оциологи€—порт—тандартизаци€—троительство“ехнологии“оргов눓уризм‘изика‘изиолог舑илософ舑инансы’ими€’оз€йство÷еннообразование„ерчениеЁкологи€ЁконометрикаЁкономикаЁлектроникаёриспунденкци€
ѕо несгруппированным данным
ѕусть имеютс€ две случайные величины, и проводитс€ их измерение.
¬ результате  независимых опытов получены,
независимых опытов получены,  пар чисел
пар чисел  ,
, 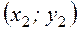 ,
,  ,
, 
Ѕудем искать линейное выборочное уравнение регрессии  на
на  в виде:
в виде:

“ак как по выборочным данным можно получить только оценки параметров, то оценку коэффициента 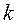 обозначим через
обозначим через  , а оценку
, а оценку 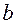 Ч через
Ч через  , то есть
, то есть  .
.
ѕараметры  и
и  находим методом наименьших квадратов по формулам:
находим методом наименьших квадратов по формулам:
 ,
,
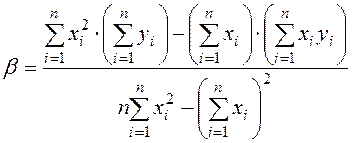
јналогично находитс€ выборочное уравнение линейной регрессии  на
на  :
:
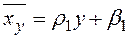 ,
,
где
 ,
,
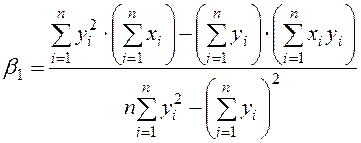 .
.
ƒл€ оценки св€зи (тесноты) между случайными величина≠ми обычно используетс€ выборочна€ ковариаци€ и выборочный коэффициент коррел€ции.
¬ыборочна€ ковариаци€ (эмпирический коррел€ционный момент) записываетс€ в виде:
 ,
,
а выборочный коэффициент коррел€ции имеет вид:
 или
или  ,
,
где  ,
,  .
.
јбсолютна€ величина (модуль) выборочного коэффициента коррел€ции не превосходит единицы, то есть  или
или  . — возрастанием
. — возрастанием  линейна€ коррел€ционна€ зависимость становитс€ более тесной, и при
линейна€ коррел€ционна€ зависимость становитс€ более тесной, и при  переходит в функциональную. ≈сли
переходит в функциональную. ≈сли  , то коррел€ционна€ св€зь испытаний
, то коррел€ционна€ св€зь испытаний  и
и  отсутствует.
отсутствует.
ѕример 11. ¬ результате независимых испытаний получены пары значений случайных величин  и
и  :
:
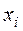
| |||||

|
¬ таблице значени€  расставлены в возрастающем пор€дке.
расставлены в возрастающем пор€дке.
Ќайти выборочное уравнение линейной регрессии и выборочный коэффициент коррел€ции. ѕостроить пр€мые регрессии  на
на  и
и  на
на  .
.
¶ —оставим таблицу подсчетов (табл.16).
“аблица 16
Ќомер опыта 
| 
| 
| 
| 
| 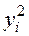
|
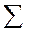
|
1) Ќаходим  ,
,  .
.
2)  ,
,  .
.
 ,
,  .
.
3) ¬ычислим эмпирический коррел€ционный момент:
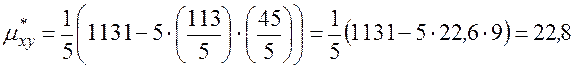 .
.
“огда коэффициент коррел€ции:  .
.
«начение  довольно близко к 1, следовательно, св€зь между случайными величинами
довольно близко к 1, следовательно, св€зь между случайными величинами  и
и  довольно тесна€.
довольно тесна€.
4) Ќайдем уравнени€ линий регрессии
 на
на  :
: 



 на
на  :
: 


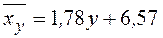
5) ѕостроим линии регрессии (–ис.6). ƒл€ этого найдем точки пересечени€ линий с ос€ми координат:
 :
:  ,
,  ;
;
 ,
, 
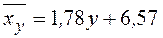 :
:  ,
,  ;
;
 ,
,  .
.

–ис.6 Ш
ѕоиск по сайту: