Однородные дифференциальные уравнения первого порядка

Определение. Уравнение вида 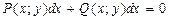называется однородным, если 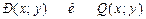- однородные функции одного измерения.

Определение. Функция f(x;y) называется однородной измерения m, если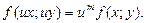

Как на практике распознать однородное уравнение? Проверка несложная, и сам алгоритм проверки можно сформулировать так:

В исходное уравнение вместо x подставляем lx, вместо y подставляем ly, производную не трогаем.

Если в результате преобразований удастся сократить ВСЕ «лямбды» (т.е. получить исходное уравнение), то данное дифференциальное уравнение является однородным.

Например, рассмотрим дифференциальное уравнение 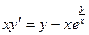и определим его тип.

Вместо x подставляем lx, вместо y подставляем ly:

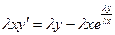
Очевидно, что лямбды сразу сокращаются в показателе степени:

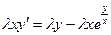
Теперь в правой части выносим лямбду за скобки:

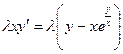
Обе части уравнения можно сократить на эту самую лямбду:

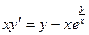
В результате все лямбды исчезли, и мы получили исходное уравнение.

Вывод: Данное уравнение является однородным.

Как же решить подобные дифференциальные уравнения? Абсолютно все однородные уравнения можно решить с помощью одной-единственной стандартной замены:

Функцию «игрек» необходимо заменить произведением некоторой функции t (тоже зависящей от «икс») и «икса»: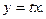

Производная 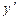при такой замене вычисляется с использованием правила дифференцирования произведения, т.е.:

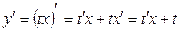
Поиск по сайту: