Примеры. a) Найти решение задачи Коши дифференциального уравнения

a) Найти решение задачи Коши дифференциального уравнения

Решение.

1.Найдем общее решение уравнения. В данном уравнении второго порядка в явном виде не участвует переменная у. Заменим первую производную у¢ новой функцией, которая зависит от «икс». Если то

Полученное дифференциальное уравнение является уравнением с разделяющимися переменными. Разделяем переменные:

Сделаем обратную замену:

2. Для нахождения частного решения, удовлетворяющего заданным начальным условиям, подставим в (*) и в (**) независимую переменную, значение функции и значение производной:

Частное решение имеет вид:

b) Найти общее решение дифференциального уравнения

Решение.

В данном уравнении второго порядка в явном виде не участвует переменная у. Заменим первую производную у¢ новой функцией, которая зависит от «икс». Если то

Цель проведенной замены очевидна – понизить степень уравнения. Получаем:

Получено линейное неоднородное уравнение первого порядка, с той лишь разницей, что вместо привычной функции «игрек» у нас функция «зет». Грубо говоря, отличие только в букве.

Линейное неоднородное уравнение первого порядка можно решить методом Бернулли (замены переменной) (Подробнее см. выше).

Тогда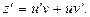

Проводим обратную замену:

Выполним проверку найденного решения. Берём полученный ответ, находим первую и вторую производные:

Подставим первую и вторую производную в исходное уравнение :

Получено верное равенство, значит, общее решение найдено правильно.

Ответ:

Поиск по сайту: