АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Дифференциальные уравнения с разделяющимися переменными

Читайте также:
  1. V2: ДЕ 54 - Дифференциальные уравнения, допускающие понижение порядка
  2. V2: ДЕ 57 - Фундаментальная система решений линейного однородного дифференциального уравнения
  3. V2: Применения уравнения Шредингера
  4. V2: Уравнения Максвелла
  5. VI Дифференциальные уравнения
  6. Алгебраические уравнения
  7. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  8. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.
  9. Вывод уравнения совершенного гидравлического прыжка.(стр11)
  10. Геометрическая оптика.отражение и преломление света. законы отражения и преломления.Зеркала и линзы.Уравнения для зеркал и линз.оптические приборы.
  11. Геометрический образ уравнения состояния.
  12. Дифференциальные автоматы.

Среди обыкновенных дифференциальных уравнений первого порядка существуют такие, в которых переменные x и y находятся по разные стороны знака равенства или их можно разнести по разные стороны знака равенства посредством преобразований. Такие уравнения называются уравнениями с разделяющимися переменными. Кроме того, некоторые дифференциальные уравнения сводятся к уравнениям с разделяющимися переменными после введения новых переменных.

Уравнения с разделяющимися переменными имеют вид:

.

- уравнение с разделенными переменными.

Общее решение дифференциальных уравнений с разделенными переменными можно найти, проинтегрировав обе части равенства:

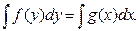
В дифференциальных уравнениях

переменные могут быть разделены, делением обеих частей уравнения на .

Соответствующее уравнение с разделенными переменными запишется как

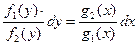
При разделении переменных следует быть очень внимательными, чтобы проводимые преобразования были эквивалентными (чтобы f2(y) и g1(x) не обращались в ноль на интервале интегрирования). В противном случае можно потерять некоторые решения.

И далее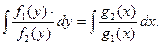

Если интегралы равенств выражаются в элементарных функциях, то можно получить общее решение дифференциального уравнения как неявно заданную функцию Ф(x, y)=0, а иногда получается выразить функцию y в явном виде.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)