Примеры. а) Найдите общее решение дифференциального уравнения

а) Найдите общее решение дифференциального уравнения

Решение.

Проинтегрируем заданное уравнение. Полученный интеграл возьмем, приведя его к табличному, воспользовавшись свойствами интеграла и дифференциала:

Таким образом, - общее решение данного уравнения.

b) Найдите общее решение дифференциального уравнения проверьте правильность результата. Найдите частное решение этого уравнения, удовлетворяющее начальному условию .

Решение.

1. Проинтегрируем заданное уравнение. Полученный интеграл возьмем по частям:

Таким образом, 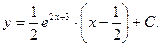- общее решение дифференциального уравнения.

2. Чтобы убедиться в правильности результата, проведем проверку. Для этого подставим полученное решение в исходное уравнение:

Следовательно, при исходное уравнение обращается в тождество 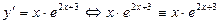, поэтому общее решение дифференциального уравнения найдено правильно.

3. Найдем частное решение уравнения, удовлетворяющее начальному условию. Иными словами, нужно найти значение константы С. Для этого подставим в найденное общее решение начальное условие:

Следовательно, подставив С = 2 в общее решение уравнения, получим частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию:

с) Найдите общее решение простейшего дифференциального уравнения

Решение.

1.Известно, что логарифмическая функция определена для положительных значений аргумента, поэтому областью определения выражения ln(x+3) является интервал x > -3. Следовательно, исходное дифференциальное уравнение имеет смысл для x > -3. При этих значениях аргумента выражение x + 3 не обращается в ноль, поэтому можно преобразовать уравнение, разделив обе его части на х + 3. Получаем:

2. Проинтегрируем полученное дифференциальное уравнение, разрешенное относительно производной и вычислим интеграл, воспользуемся методом подведения под знак дифференциала:

Т.о., - общее решение дифференциального уравнения при x > -3.

Поиск по сайту: