 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Примеры. а) Найдите общее решение дифференциального уравнения с разделенными переменными
а) Найдите общее решение дифференциального уравнения с разделенными переменными 
Решение.
Проинтегрируем обе части равенства: 
По сути, мы уже получили общее решение исходного дифференциального уравнения, так как свели задачу решения дифференциального уравнения к уже известной задаче нахождения неопределенных интегралов. Однако, эти неопределенные интегралы выражаются в элементарных функциях, и мы можем взять их:
где С1 и С2 – произвольные постоянные.
Функция 
, которая является общим решением исходного дифференциального уравнения с разделенными переменными, задана неявно. Ответ можно оставить в таком виде. Но в нашем случае искомую функцию y можно выразить явно через аргумент x:
То есть, функция 
является общим решением исходного дифференциального уравнения.
b) Решить дифференциальное уравнение 
Решение.
1.В первую очередь нужно переписать производную немного в другом виде: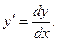 
Переписываем уравнение: 
.
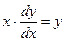2.На втором этапе всегда смотрим, нельзя ли разделить переменные? Что значит разделить переменные? Грубо говоря, в левой части нам нужно оставить только «игреки», а в правой части организовать только «иксы». Разделение переменных выполняется с помощью алгебраических преобразований: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т.п.
Дифференциалы 
и 
– это полноправные множители. В рассматриваемом примере переменные легко разделяются умножением обеих частей уравнения на и делением обеих же частей уравнения на х:
Переменные разделены. В левой части – только «игреки», в правой части – только «иксы». Получили уравнение с разделенными переменными.
3. Следующий этап – интегрирование дифференциального уравнения:
Интегралы нужно взять, тем более в данном случае они табличные:
К любой первообразной приписывается константа. Здесь два интеграла, но константу С достаточно записать один раз. Почти всегда её приписывают в правой части.
Строго говоря, после того, как взяты интегралы, дифференциальное уравнение считается решенным. Единственное, у нас «игрек» не выражен через «икс», то есть решение представлено в неявном виде. То есть, – это общий интеграл.
Теперь нужно попробовать найти общее решение, то есть попытаться представить функцию в явном виде.
Когда в правой части после интегрирования появляется логарифм, то константу почти всегда целесообразно записать тоже под логарифмом. Это нужно для того, чтобы легче было выразить «игрек».
То есть, вместо записи обычно пишут 
.
Здесь 
– это такая же полноценная константа, как и С.
Используя свойство логарифмов: 
, получим 
.
Теперь логарифмы и модули можно убрать с обеих частей 
.
Функция представлена в явном виде. Это и есть общее решение.
с) Найти частное решение дифференциального уравнения 
удовлетворяющее начальному условию y(0)=2.
Решение.
1.Сначала находим общее решение. В уравнении нет переменной «икс», но это не должно смущать, главное, в нём есть первая производная.
Переписываем производную в нужном виде:
Разделяем переменные: «игреки» – налево, «иксы» – направо
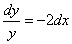
Интегрируем уравнение:
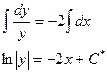
Общий интеграл получен. Обратите внимание на константу. Дело в том, что очень скоро она превратится в другую константу.
Преобразуем общий интеграл в общее решение (выразим «игрек» в явном виде). Вспомним определение логарифма 
. В данном случае:
Константу в показателе степени обычно спускают, используя свойство степеней,
Если С*– это константа, то еС* – тоже некоторая константа, которую обозначим через букву С. Получим:
2. Теперь нужно найти частное решение, удовлетворяющее заданному начальному условию y(0)=2.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку:
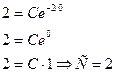
Частное решение исходного уравнения: 
.
Выполним проверку. Возьмем полученное частное решение и найдем производную:
Подставим и 
в исходное уравнение 
:
Получено верное равенство, следовательно, частное решение найдено правильно.
Поиск по сайту: