Решение. Составим и решим характеристическое уравнение

Составим и решим характеристическое уравнение

Характеристическое уравнение имеет два различных действительных корня

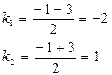
Общее решение имеет вид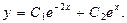

Выполним проверку. Берем ответ и находим производную:

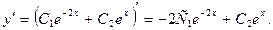
Находим вторую производную:

Подставляем найденные значения производных в левую часть исходного уравнения:

Получено тождество, значит, общее решение 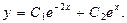найдено правильно.

b) Решить дифференциальное уравнение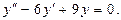

Решение.

Составим и решим характеристическое уравнение:

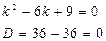
Здесь можно вычислить дискриминант, получить ноль и найти кратные корни. Но можно применить известную формулу сокращенного умножения:

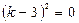
Получены два кратных действительных корня k_1,2 =3

Общее решение имеет вид: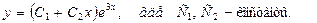

с) Решить однородное дифференциальное уравнение второго порядка

Решение.

Составим и решим характеристическое уравнение:

Характеристическое уравнение имеет сопряженные комплексные корни:

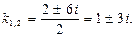
Общее решение имеет вид:

d) Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям

Решение.

1.Cоставим и решим характеристическое уравнение:

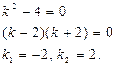
Получены два различных действительных корня, поэтому общее решение:

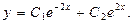
2.Теперь нужно найти частное решение, соответствующее заданным начальным условиям. Алгоритм нахождения частного решения следующий:

Сначала используем начальное условие :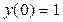

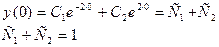
Далее берём наше общее решение и находим производную:

Используем второе начальное условие

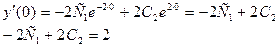
Составим и решим систему из двух найденных уравнений:

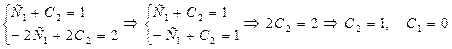
Подставляем найденные значения констант в общее решение:

Получено частное решение.

Проверка осуществляется по следующей схеме:

Сначала проверим, выполняется ли начальное условие :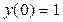

– начальное условие выполнено.

Находим первую производную от ответа:

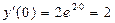– второе начальное условие тоже выполнено.

Находим вторую производную:

Подставим и в левую часть исходного дифференциального уравнения :

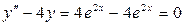что и требовалось проверить.

Таким образом, частное решение найдено, верно.

Поиск по сайту: