Линейные дифференциальные уравнения первого порядка

Определение. Дифференциальное уравнение вида называется линейным. Если 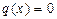- уравнение называется линейным однородным и является уравнением с разделяющимися переменными, если - уравнение называется линейным неоднородным.

Характерные черты линейного уравнения:

1) В линейное уравнение входит первая производная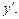

2) В линейное уравнение входит произведение , где у – функция, р(х) – выражение, зависящее только от «икс».

3) В линейное уравнение входит выражение 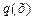, тоже зависящее только от «икс». В частности, 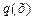может быть константой.

Примечание: Разумеется, в практических примерах эти три слагаемых не обязаны располагаться именно в таком порядке, их спокойно можно переносить из части со сменой знака.

Некоторые частные модификации линейного уравнения:

· Выражение 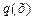может быть некоторой константой k, в этом случае линейное уравнение принимает вид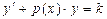

· Выражение тоже может быть некоторой константой k, тогда линейное уравнение принимает вид .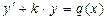

· Рядом с производной может находиться множитель , зависящий только от «икс» – это тоже линейное уравнение.

Способы решения линейных уравнений:

· метод Лагранжа (метод вариации произвольной постоянной);

· метод Бернулли (метод замены переменной).

Поиск по сайту: