Простейшие дифференциальные уравнения 1-го порядка

Отличительной чертой простейших дифференциальных уравнений является отсутствие в уравнении неизвестной функции. Такие уравнения либо уже разрешены относительно производной, т.е. имеют вид или , либо их можно разрешить относительно производной, т.е.

Простейшее дифференциальное уравнение можно разрешить относительно производной, разделив обе части равенства на f(x). Такое преобразование будет эквивалентным, если f(x) не обращается в ноль ни при каких x из интервала интегрирования дифференциального уравнения.

Возможны случаи, когда при некоторых значениях аргумента x ∈ X функции f(x) и g(x) одновременно обращаются в ноль. Для таких значений x общим решением дифференциального уравнения является любая функция y, определенная в них, так как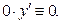

Если для некоторых значений аргумента x ∈ X выполняются условия ,

то в этом случае уравнение решений не имеет.

Для остальных x из интервала X общее решение дифференциального уравнения определяется из преобразованного уравнения

Общее решение простейших дифференциальных уравнений можно отыскать, проинтегрировав обе части этого уравнения. Получим:

Итак, y=F(x)+C – искомое общее решение, где F(x) – одна из первообразных функции f(x), а С – произвольная постоянная.

Если требуется найти частное решение простейшего дифференциального уравнения, удовлетворяющее начальному условию y(x₀) = y₀, то после нахождения общего решения y = F(x) + C, еще нужно вычислить значение постоянной C = C₀, используя начальное условие. То есть, константа C = C₀ определяется из уравнения F(x₀) + C = y₀, и искомое частное решение дифференциального уравнения будет иметь вид y = F(x) + C₀.

Поиск по сайту: