Рассмотрим метод Бернулли. Он заключается в выражении неизвестной функции через произведение двух, неизвестных на первом этапе, функций, зависящих от «икс», т.е

Тогда

Исходное уравнение принимает вид

Преобразуем немного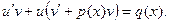

Поскольку одна из неизвестных функций (например, v) может быть выбрана совершенно произвольно, так как лишь произведение uv должно удовлетворять исходному уравнению, выберем v таким образом, что

Решая это уравнение, которое является уравнением с разделяющими переменными, получаем:

Обратите внимание, что на данном этапе решения константа не учитывается. Найдено одно из частных решений уравнения

Далее решаем уравнение Это тоже уравнение с разделяющими переменными.

Общее решение исходного дифференциального уравнения будет иметь вид:

Поиск по сайту: