 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Примеры. 1.Проверим, является ли данное уравнение однородным
а) Решить уравнение: 
.
Решение.
1.Проверим, является ли данное уравнение однородным. Подставим в уравнение вместо x - lx, вместо y подставляем ly.
Постоянная l полностью сократилась. Поэтому уравнение является однородным.
2.Делаем замену 
; 
и подставляем в исходное уравнение:
Преобразуем полученное уравнение:
3.Получили уравнение с разделяющимися переменными. Разделим переменные, умножив обе части уравнения на 
и разделим на 
При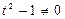 
уравнение принимает вид:
Интегрируем обе части полученного уравнения с разделенными переменными:
Сделаем обратную замену 
:
Полученная функция, которая задана неявно, является общим интегралом исходного дифференциального уравнения. Попытаемся выразить у.
Умножим обе части на x:
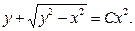
Выразим корень квадратный:
Возведем обе части уравнения в квадрат:
Разделим на x2:
Получили решение уравнения при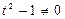
4. Теперь рассмотрим случай 
, т.е. 
Корни этого уравнения 
являются решениями исходного уравнения и не входят в полученное решение . Поэтому к общему интегралу добавим решения .
Ответ:
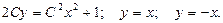
b) Проверить уравнение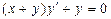 
на однородность и найти его общий интеграл. Выполнить проверку.
Решение.
1.Проверим, является ли данное уравнение однородным. Подставим в уравнение вместо x - lx, вместо y подставляем ly:
Все лямбды сократились, и получилось исходное уравнение, значит, данное ДУ является однородным.
2.Проведем замену: и максимально упростим уравнение:
3.Разделяем переменные, слева собираем «тэ», справа – «иксы»:
Интегрируем:
Воспользуемся приемом подведения под знак дифференциала:
Получили общий интеграл исходного дифференциального уравнения. Максимально упрощаем его. Если есть дроби, то от них лучше избавиться, умножаем каждую часть на 2:
Константу 
лучше переобозначить через 
:
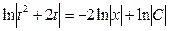
Собираем в правой части всё под логарифм, затем избавляемся от логарифмов:
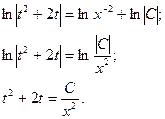
Выполняем обратную замену:
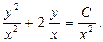
Умножаем все слагаемые на 
:
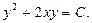
Ответ: общий интеграл: 
.
Проверка: Дифференцируем общий интеграл:
Получено исходное дифференциальное уравнение, значит, решение найдено верно.
Поиск по сайту: