Примеры. Интегрируя обе части уравнения первый раз, получаем:

а) Решить уравнение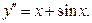

Решение.

Интегрируя обе части уравнения первый раз, получаем:

Общее решение данного уравнения получаем, интегрируя второй раз:

b) Решить уравнение

Решение.

Преобразуем уравнение

Уравнение приобрело вид

Дважды интегрируем правую часть:

Получили общее решение данного дифференциального уравнения.

c) Решить задачу Коши

Решение.

1.Найдем общее решение данного дифференциального уравнения, дважды проинтегрировав правую часть уравнения:

2.Для нахождения константы С₁ подставим данные в выражение для производной первого порядка:

3. Для нахождения константы С₂ подставим данные и найденную константу С₁ в общее решение дифференциального уравнения:

Частное решение данного дифференциального уравнения, удовлетворяющего заданным начальным условиям, будет иметь вид:

Поиск по сайту: