Примеры. а) Найти общее решение дифференциального уравнения

а) Найти общее решение дифференциального уравнения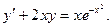

Решение.

Данное уравнение имеет «классический» вид линейного уравнения.

Проведем замену: и подставим в исходное уравнение:

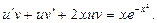
После подстановки проведем вынесение множителя за скобки:

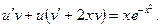
Составляем систему. Для этого приравниванием к нулю то, что находится в скобках: 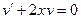, автоматически получая и второе уравнение системы:

В результате:

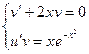
Из первого уравнения найдем функцию v:

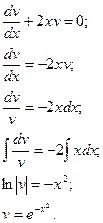
Найденную функцию v подставим во второе уравнение системы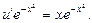

Теперь находим функцию u.

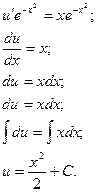
Обе функции найдены. Таким образом, общее решение:

.

b) Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию y(1)=e (такая постановка вопроса также называется задачей Коши).

Поиск по сайту: