ББК 15.56 2 страница

Испарением называется фазовый переход из жидкого состояния в газообразное. С точки зрения молекулярно-кинетической теории, испарение – это процесс, при котором с поверхности жидкости вылетают наиболее быстрые молекулы, кинетическая энергия которых превышает энергию их связи с остальными молекулами жидкости. Это приводит к уменьшению средней кинетической энергии оставшихся молекул, т. е. к охлаждению жидкости (если нет подвода энергии от окружающих тел).

Конденсация – это процесс, обратный процессу испарения. При конденсации молекулы пара возвращаются в жидкость. В закрытом сосуде жидкость и ее пар могут находиться в состоянии динамического равновесия, когда число молекул, вылетающих из жидкости, равно числу молекул, возвращающихся в жидкость из пара, т. е. когда скорости процессов испарения и конденсации одинаковы. Такую систему называют двухфазной. Пар, находящийся в равновесии со своей жидкостью, называют насыщенным.

Число молекул, вылетающих с единицы площади поверхности жидкости за одну секунду, зависит от температуры жидкости. Число молекул, возвращающихся из пара в жидкость, зависит от концентрации молекул пара и от средней скорости их теплового движения, которая определяется температурой пара.

Модель. Испарение и конденсация.

Отсюда следует, что для данного вещества концентрация молекул пара при равновесии жидкости и ее пара определяется их равновесной температурой. Установление динамического равновесия между процессами испарения и конденсации при повышении температуры происходит при более высоких концентрациях молекул пара. Так как давление газа (пара) определяется его концентрацией и температурой, то можно сделать вывод: давление насыщенного пара p ₀ данного вещества зависит только от его температуры и не зависит от объема. Поэтому изотермы реальных газов на плоскости (p, V) содержат горизонтальные участки, соответствующие двухфазной системе (рис. 3.4.1).

Рисунок 3.4.1. Изотермы реального газа. Область I – жидкость, область II – двухфазная система «жидкость + насыщенный пар», область III – газообразное вещество. K – критическая точка.

При повышении температуры давление насыщенного пара и его плотность возрастают, а плотность жидкости уменьшается из-за теплового расширения. При температуре, равной критической температуре T_кр для данного вещества, плотности пара и жидкости становятся одинаковыми. При T > T_кр исчезают физические различия между жидкостью и ее насыщенным паром.

Если изотермически сжимать ненасыщенный пар при T < T_кр, то его давление будет возрастать, пока не станет равным давлению насыщенного пара. При дальнейшем уменьшении объема на дне сосуда образуется жидкость и устанавливается динамическое равновесие между жидкостью и ее насыщенным паром. С уменьшением объема все большая часть пара конденсируется, а его давление остается неизменным (горизонтальный участок на изотерме). Когда весь пар превращается в жидкость, давление резко возрастает при дальнейшем уменьшении объема вследствие малой сжимаемости жидкости.

Из газообразного состояния в жидкое можно перейти, минуя двухфазную область. Для этого нужно совершить процесс в обход критической точки K. Один из возможных процессов такого рода показан на рис. 3.4.1 ломаной линией ABC.

Модель. Изотермы реального газа.

В атмосферном воздухе всегда присутствуют пары воды при некотором парциальном давлении p, которое, как правило, меньше давления насыщенного пара p₀. Отношение p / p₀, выраженное в процентах, называется относительной влажностью воздуха.

Ненасыщенный пар можно теоретически описывать с помощью уравнения состояния идеального газа при обычных для реальных газов ограничениях: давление пара должно быть не слишком велико (практически p ≤ (10⁶–10⁷) Па), а его температура выше некоторого определенного для каждого вещества значения. К насыщенному пару также можно приближенно применять законы идеального газа при условии, что для каждой температуры T давление p₀ насыщенного пара определяется по кривой равновесия p₀(T) для данного вещества.

Давление p₀ насыщенного пара очень быстро возрастает с ростом температуры T. Зависимость p₀(T) нельзя получить из законов идеального газа. Давление газа при постоянной концентрации молекул растет прямо пропорционально температуре. В насыщенном паре при повышении температуры возрастает не только средняя кинетическая энергия движения молекул, но и их концентрация. Поэтому давление насыщенного пара при повышении температуры возрастает быстрее, чем давление идеального газа при постоянной концентрации молекул.

Испарение может происходить не только с поверхности, но и в объеме жидкости. В жидкости всегда имеются мельчайшие пузырьки газа. Если давление насыщенного пара жидкости равно внешнему давлению (т. е. давлению газа в пузырьках) или превышает его, жидкость будет испаряться внутрь пузырьков. Пузырьки, наполненные паром, расширяются и всплывают на поверхность. Этот процесс называется кипением. Таким образом, кипение жидкости начинается при такой температуре, при которой давление ее насыщенных паров становится равным внешнему давлению.

В частности, при нормальном атмосферном давлении вода кипит при температуре 100 °С. Это значит, что при такой температуре давление насыщенных паров воды равно 1 атм. При подъеме в горы атмосферное давление уменьшается, и поэтому температура кипения воды понижается (приблизительно на 1 °С на каждые 300 метров высоты). На высоте 7 км давление составляет примерно 0,4 атм, и температура кипения понижается до 70 °С.

В герметически закрытом сосуде жидкость кипеть не может, т. к. при каждом значении температуры устанавливается равновесие между жидкостью и ее насыщенным паром. По кривой равновесия p₀(T) можно определять температуры кипения жидкости при различных давлениях.

Изображенная на рис. 3.4.1 картина изотерм реального газа описывает процессы испарения и конденсации, т. е. фазовый переход между газообразной и жидкой фазами вещества. На самом деле эта картина является неполной, т. к. из газообразного и жидкого состояний любое вещество может перейти в твердое состояние. При заданной температуре T термодинамическое равновесие между двумя фазами одного и того же вещества возможно лишь при определенном значении давления в системе. Зависимость равновесного давления от температуры называется кривой фазового равновесия. Примером может служить кривая равновесия p₀(T) насыщенного пара и жидкости. Если кривые равновесия между различными фазами данного вещества построить на плоскости (p, T), то они разбивают эту плоскость на отдельные области, в которых вещество существует в однородном агрегатном состоянии – твердом, жидком или газообразном (рис. 3.4.2). Изображенные в координатной системе (p, T) кривые равновесия называются фазовой диаграммой.

Рисунок 3.4.2. Типичная фазовая диаграмма вещества. K – критическая точка, T – тройная точка. Область I – твердое тело, область II – жидкость, область III – газообразное вещество.

Кривая OT, соответствующая равновесию между твердой и газообразной фазами, называется кривой сублимации. Кривая TK равновесия между жидкостью и паром называется кривой испарения, она обрывается в критической точке K. Кривая TM равновесия между твердым телом и жидкостью называется кривой плавления.

Кривые равновесия сходятся в точке T, в которой могут сосуществовать в равновесии все три фазы. Эта точка называется тройной точкой.

Для многих веществ давление p_тр в тройной точке меньше 1 атм ≈ 10⁵ Па. Такие вещества при нагревании при атмосферном давлении плавятся. Например, тройная точка воды имеет координаты T_тр = 273,16 К, p_тр = 6,02·10² Па. Эта точка используется в качестве опорной для калибровки абсолютной температурной шкалы Кельвина (см. §3.2). Существуют, однако, и такие вещества, у которых p_тр превышает 1 атм. Так для углекислоты (CO₂) давление p_тр = 5,11 атм и температура T_тр = 216,5 К. Поэтому при атмосферном давлении твердая углекислота может существовать только при низкой температуре, а в жидком состоянии при p = 1 атм она вообще не существует. В равновесии со своим паром при атмосферном давлении углекислота находится при температуре 173 К или –80 °С в твердом состоянии. Это широко применяемый «сухой лед», который никогда не плавится, а только испаряется (сублимирует).

3.5. Свойства жидкостей. Поверхностное натяжение window.top.document.title = "3.5. Свойства жидкостей. Поверхностное натяжение";

Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. В отличие от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия. Однако, время от времени любая молекула может переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах (см. §3.6), и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей. Из-за сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные (неустойчивые) упорядоченные группы, содержащие несколько молекул. Это явление называется ближним порядком (рис. 3.5.1).

Рисунок 3.5.1. Пример ближнего порядка молекул жидкости и дальнего порядка молекул кристаллического вещества: 1 – вода; 2 – лед.

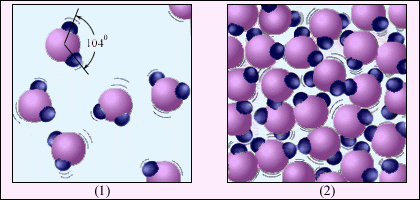
Рис. 3.5.2 иллюстрирует отличие газообразного вещества от жидкости на примере воды. Молекула воды H₂O состоит из одного атома кислорода и двух атомов водорода, расположенных под углом 104°. Среднее расстояние между молекулами пара в десятки раз превышает среднее расстояние между молекулами воды. В отличие от рис. 3.5.1, где молекулы воды изображены в виде шариков, рис. 3.5.2 дает представление о структуре молекулы воды.

Рисунок 3.5.2. Водяной пар (1) и вода (2). Молекулы воды увеличены примерно в 5·107 раз.

Вследствие плотной упаковки молекул сжимаемость жидкостей, т. е. изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах.

Жидкости, как и твердые тела, изменяют свой объем при изменении температуры. Для не очень больших интервалов температур относительное изменение объема ΔV / V₀ пропорционально изменению температуры ΔT:

Коэффициент β называют температурным коэффициентом объемного расширения. Этот коэффициент у жидкостей в десятки раз больше, чем у твердых тел. У воды, например, при температуре 20 °С β_в ≈ 2·10^–4 К^–1, у стали β_ст ≈ 3,6·10^–5 К^–1, у кварцевого стекла β_кв ≈ 9·10^–6 К^–1.

Тепловое расширение воды имеет интересную и важную для жизни на Земле аномалию. При температуре ниже 4 °С вода расширяется при понижении температуры (β < 0). Максимум плотности ρ_в = 10³ кг/м³ вода имеет при температуре 4 °С.

При замерзании вода расширяется, поэтому лед остается плавать на поверхности замерзающего водоема. Температура замерзающей воды подо льдом равна 0 °С. В более плотных слоях воды у дна водоема температура оказывается порядка 4 °С. Благодаря этому может существовать жизнь в воде замерзающих водоемов.

Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Если молекула переместиться с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (т. е. увеличить площадь поверхности жидкости), надо затратить положительную работу внешних сил ΔA_внеш, пропорциональную изменению ΔS площади поверхности:

Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.

В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м²) или в ньютонах на метр (1 Н/м = 1 Дж/м²).

Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия E_p поверхности жидкости пропорциональна ее площади:

Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения.

Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку, с той только разницей, что упругие силы в пленке зависят от площади ее поверхности (т. е. от того, как пленка деформирована), а силы поверхностного натяжения не зависят от площади поверхности жидкости.

Некоторые жидкости, как, например, мыльная вода, обладают способностью образовывать тонкие пленки. Всем хорошо известные мыльные пузыри имеют правильную сферическую форму – в этом тоже проявляется действие сил поверхностного натяжения. Если в мыльный раствор опустить проволочную рамку, одна из сторон которой подвижна, то вся она затянется пленкой жидкости (рис. 3.5.3).

Рисунок 3.5.3. Подвижная сторона проволочной рамки в равновесии под действием внешней силы 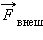и результирующей сил поверхностного натяжения .

Силы поверхностного натяжения стремятся сократить поверхность пленки. Для равновесия подвижной стороны рамки к ней нужно приложить внешнюю силу Если под действием силы перекладина переместиться на Δx, то будет произведена работа ΔA_внеш = F_внешΔx = ΔE_p = σΔS, где ΔS = 2LΔx – приращение площади поверхности обеих сторон мыльной пленки. Так как модули сил 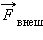и одинаковы, можно записать:

Коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.

Из-за действия сил поверхностного натяжения в каплях жидкости и внутри мыльных пузырей возникает избыточное давление Δp. Если мысленно разрезать сферическую каплю радиуса R на две половинки, то каждая из них должна находиться в равновесии под действием сил поверхностного натяжения, приложенных к границе 2πR разреза, и сил избыточного давления, действующих на площадь πR² сечения (рис. 3.5.4). Условие равновесия записывается в виде

Отсюда избыточное давление внутри капли равно

Рисунок 3.5.4. Сечение сферической капли жидкости.

Избыточное давление внутри мыльного пузыря в два раза больше, так как пленка имеет две поверхности:

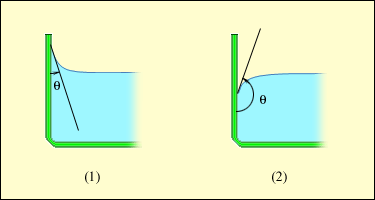
Вблизи границы между жидкостью, твердым телом и газом форма свободной поверхности жидкости зависит от сил взаимодействия молекул жидкости с молекулами твердого тела (взаимодействием с молекулами газа (или пара) можно пренебречь). Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела. В этом случае жидкость подходит к поверхности твердого тела под некоторым острым углом θ, характерным для данной пары жидкость – твердое тело. Угол θ называется краевым углом. Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол θ оказывается тупым (рис. 3.5.5). В этом случае говорят, что жидкость не смачивает поверхность твердого тела. При полном смачивании θ = 0, при полном несмачивании θ = 180°.

Рисунок 3.5.5. Краевые углы смачивающей (1) и несмачивающей (2) жидкостей.

Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются.

На рис. 3.5.6 изображена капиллярная трубка некоторого радиуса r, опущенная нижним концом в смачивающую жидкость плотности ρ. Верхний конец капилляра открыт. Подъем жидкости в капилляре продолжается до тех пор, пока сила тяжести действующая на столб жидкости в капилляре, не станет равной по модулю результирующей F_н сил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: F_т = F_н, где F_т = mg = ρhπr²g, F_н = σ2πr cos θ.

Отсюда следует:

Рисунок 3.5.6. Подъем смачивающей жидкости в капилляре.

При полном смачивании θ = 0, cos θ = 1. В этом случае

При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.

Вода практически полностью смачивает чистую поверхность стекла. Наоборот, ртуть полностью не смачивает стеклянную поверхность. Поэтому уровень ртути в стеклянном капилляре опускается ниже уровня в сосуде.

3.6. Кристаллические и аморфные тела window.top.document.title = "3.6. Кристаллические и аморфные тела";

По своим физическим свойствам и молекулярной структуре твердые тела разделяются на два класса – аморфные и кристаллические тела.

Характерной особенностью аморфных тел является их изотропность, т. е. независимость всех физических свойств (механических, оптических и т. д.) от направления. Молекулы и атомы в изотропных твердых телах располагаются хаотично, образуя лишь небольшие локальные группы, содержащие несколько частиц (ближний порядок). По своей структуре аморфные тела очень близки к жидкостям (см. §3.5). Примерами аморфных тел могут служить стекло, различные затвердевшие смолы (янтарь), пластики и т. д. Если аморфное тело нагревать, то оно постепенно размягчается, и переход в жидкое состояние занимает значительный интервал температур.

В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества. Например, решетка поваренной соли содержит ионы Na⁺ и Cl^–, не объединенные попарно в молекулы NaCl (рис. 3.6.1). Такие кристаллы называются ионными.

Рисунок 3.6.1. Кристаллическая решетка поваренной соли.

В каждой пространственной решетке можно выделить структурный элемент минимального размера, который называется элементарной ячейкой. Вся кристаллическая решетка может быть построена путем параллельного переноса (трансляции) элементарной ячейки по некоторым направлениям.

Теоретически доказано, что всего может существовать 230 различных пространственных кристаллических структур. Большинство из них (но не все) обнаружены в природе или созданы искусственно.

Кристаллические решетки металлов часто имеют форму шестигранной призмы (цинк, магний), гранецентрированного куба (медь, золото) или объемно центрированного куба (железо).

Кристаллические тела могут быть монокристаллами и поликристаллами. Поликристаллические тела состоят из многих сросшихся между собой хаотически ориентированных маленьких кристалликов, которые называются кристаллитами. Большие монокристаллы редко встречаются в природе и технике. Чаще всего кристаллические твердые тела, в том числе и те, которые получаются искусственно, являются поликристаллами.

В отличие от монокристаллов, поликристаллические тела изотропны, т. е. их свойства одинаковы во всех направлениях. Поликристаллическое строение твердого тела можно обнаружить с помощью микроскопа, а иногда оно видно и невооруженным глазом (чугун).

Многие вещества могут существовать в нескольких кристаллических модификациях (фазах), отличающихся физическими свойствами. Это явление называется полиморфизмом. Переход из одной модификации в другую называется полиморфным переходом. Интересным и важным примером полиморфного перехода является превращение графита в алмаз. Этот переход при производстве искусственных алмазов осуществляется при давлениях 60–100 тысяч атмосфер и температурах 1500–2000 К.

Структуры кристаллических решеток экспериментально изучаются с помощью дифракции рентгеновского излучения на монокристаллах или поликристаллических образцах.

На рис. 3.6.2 приведены примеры простых кристаллических решеток. Следует помнить, что частицы в кристаллах плотно упакованы, так что расстояние между их центрами приблизительно равно размеру частиц. В изображении кристаллических решеток указывается только положение центров частиц.

Рисунок 3.6.2. Простые кристаллические решетки: 1 – простая кубическая решетка; 2 – гранецентрированная кубическая решетка; 3 – объемноцентрированная кубическая решетка; 4 – гексагональная решетка.

В простой кубической решетке частицы располагаются в вершинах куба. В гранецентрированной решетке частицы располагаются не только в вершинах куба, но и в центрах каждой его грани. Изображенная на рис. 3.6.1 решетка поваренной соли состоит из двух вложенных друг в друга гранецентрированных решеток, состоящих из Na⁺ и Cl^–. В объемноцентрированной кубической решетке дополнительная частица располагается в центре каждой элементарной кубической ячейки.

Кристаллические структуры металлов имеют важную особенность. Положительно заряженные ионы металла, образующие кристаллическую решетку, удерживаются вблизи положений равновесия силами взаимодействия с «газом свободных электронов» (рис. 3.6.3). Электронный газ образуется за счет одного или нескольких электронов, отданных каждым атомом. Свободные электроны способны блуждать по всему объему кристалла.

Рисунок 3.6.3. Структура металлического кристалла.

3.7. Деформация window.top.document.title = "3.7. Деформация";

В твердых телах – аморфных и кристаллических – частицы (молекулы, атомы, ионы) совершают тепловые колебания около положений равновесия, в которых энергия их взаимодействия минимальна. При увеличении расстояния между частицами возникают силы притяжения, а при уменьшении – силы отталкивания (см. §3.1). Силы взаимодействия между частицами обусловливают механические свойства твердых тел.

Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними.

Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рис. 3.7.1.

Рисунок 3.7.1. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия.

Простейшим видом деформации является деформация растяжения или сжатия. Ее можно характеризовать абсолютным удлинением Δl, возникающим под действием внешней силы Связь между Δl и F зависит не только от механических свойств вещества, но и от геометрических размеров тела (его толщины и длины).

Поиск по сайту: