 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ББК 15.56 5 страница
|
В каком бы направлении ни обходился цикл Карно (по или против часовой стрелки) величины Q1 и Q2 всегда имеют разные знаки. Поэтому можно записать
|
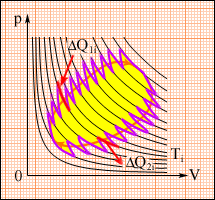
Это соотношение может быть обобщено на любой замкнутый обратимый процесс, который можно представить как последовательность малых изотермических и адиабатических участков (рис. 3.12.3).
|
| Рисунок 3.12.3. Произвольный обратимый цикл как последовательность малых изотермических и адиабатических участков. |
При полном обходе замкнутого обратимого цикла
|
где ΔQi = ΔQ1i + ΔQ2i – количество теплоты, полученное рабочим телом на двух изотермических участках при температуре Ti. Для того, чтобы такой сложный цикл провести обратимым путем, необходимо рабочее тело приводить в тепловой контакт со многими тепловыми резервуарами с температурами Ti. Отношение ΔQi / Ti называется приведенным теплом. Полученная формула показывает, что полное приведенное тепло на любом обратимом цикле равно нулю. Эта формула позволяет ввести новую физическую величину, которая называется энтропией и обозначается буквой S (Р. Клаузиус, 1865 г.). Если термодинамическая система переходит из одного равновесного состояния в другое, то ее энтропия изменяется. Разность значений энтропии в двух состояниях равна приведенному теплу, полученному системой при обратимом переходе из одного состояния в другое.
|
В случае обратимого адиабатического процесса ΔQi = 0 и, следовательно, энтропия S остается неизменной. Выражение для изменения энтропии ΔS при переходе неизолированной системы из одного равновесного состояния (1) в другое равновесное состояние (2) может быть записано в виде
|
Энтропия определена с точностью до постоянного слагаемого, так же, как, на-пример, потенциальная энергия тела в силовом поле. Физический смысл имеет разность ΔS энтропии в двух состояниях системы. Чтобы определить измене-ние энтропии в случае необратимого перехода системы из одного состояния в другое, нужно придумать какой-нибудь обратимый процесс, связывающий начальное и конечное состояния, и найти приведенное тепло, полученное системой при таком переходе.
|
| Модель. Энтропия и фазовые переходы. |
Рис. 3.12.4 иллюстрирует необратимый процесс расширения газа «в пустоту» в отсутствие теплообмена. Только начальное и конечное состояния газа в этом процессе являются равновесными, и их можно изобразить на диаграмме (p, V). Точки (a) и (b), соответствующие этим состояниям, лежат на одной изотерме. Для вычисления изменения ΔS энтропии можно рассмотреть обратимый изотермический переход из (a) в (b). Поскольку при изотермическом расширении газ получает некоторое количество теплоты от окружающих тел Q > 0, можно сделать вывод, что при необратимом расширении газа энтропия возросла: ΔS > 0.
|
Рисунок 3.12.4.
Расширение газа в «пустоту». Изменение энтропии  где A = Q – работа газа при обратимом изотермическом расширении.
|
Другой пример необратимого процесса – теплообмен при конечной разности температур. На рис. 3.12.5 изображены два тела, заключенные в адиабатичес-кую оболочку. Начальные температуры тел T1 и T2 < T1. При теплообмене температуры тел постепенно выравниваются. Более теплое тело отдает некоторое количество теплоты, а более холодное – получает. Приведенное тепло, получаемое холодным телом, превосходит по модулю приведенное тепло, отдаваемое горячим телом. Отсюда следует, что изменение энтропии замкнутой системы в необратимом процессе теплообмена ΔS > 0.
|
| Рисунок 3.12.5. Теплообмен при конечной разности температур: a – начальное состояние; b – конечное состояние системы. Изменение энтропии ΔS > 0. |
Рост энтропии является общим свойством всех самопроизвольно протекающих необратимых процессов в изолированных термодинамических системах. При обратимых процессах в изолированных системах энтропия не изменяется:
|
Это соотношение принято называть законом возрастания энтропии.
При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо остается неизменной, либо увеличивается.
Таким образом, энтропия указывает направление самопроизвольно протекаю-щих процессов. Рост энтропии указывает на приближение системы к состоя-нию термодинамического равновесия. В состоянии равновесия энтропия принимает максимальное значение. Закон возрастания энтропии можно принять в качестве еще одной формулировки второго закона термодинамики.
В 1878 году Л. Больцман дал вероятностную трактовку понятия энтропии. Он предложил рассматривать энтропию как меру статистического беспорядка в замкнутой термодинамической системе. Все самопроизвольно протекающие процессы в замкнутой системе, приближающие систему к состоянию равновесия и сопровождающиеся ростом энтропии, направлены в сторону увеличения вероятности состояния.
Всякое состояние макроскопической системы, содержащей большое число частиц, может быть реализовано многими способами. Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние. По определению термодинамическая вероятность W >> 1.
Например, если в сосуде находится 1 моль газа, то возможно огромное число N способов размещения молекулы по двум половинкам сосуда: 
где 
– число Авогадро. Каждый из них является микросостоянием. Только одно из микросостояний соответствует случаю, когда все молекулы соберутся в одной половинке (например, правой) сосуда. Вероятность такого события практически равна нулю. Наибольшее число микросостояний соответствует равновесному состоянию, при котором молекулы равномерно распределены по всему объему. Поэтому равновесное состояние является наиболее вероятным. Равновесное состояние с другой стороны является состоянием наибольшего беспорядка в термодинамической системе и состоянием с максимальной энтропией.
Согласно Больцману, энтропия S системы и термодинамическая вероятность W связаны между собой следующим образом:
|
где k = 1,38·10–23 Дж/К – постоянная Больцмана. Таким образом, энтропия опре-деляется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рас-сматриваться как мера вероятности состояния термодинамической системы.
Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Такие отклонения называются флуктуациями. В системах, содержащих большое число частиц, значительные отклонения от состояния равновесия имеют чрезвычайно малую вероятность.
R.3.1. Некоторые постоянные элементов window.top.document.title = "R.3.1. Некоторые постоянные элементов";
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица R.3.1.1. Некоторые постоянные элементов (при давлении 760 мм рт. ст.) ρ – плотность, CP – молярная теплоемкость (при 25 °С); tпл и tкип – температуры плавления и кипения; q – молярная теплота плавления; r – молярная теплота парообразования; λ – теплопроводность (значения приведены для температур, указанных в скобках); α – температурный коэффициент линейного расширения изотропных элементов при 0 °C. |
R.3.2. Некоторые постоянные твердых тел window.top.document.title = "R.3.2. Некоторые постоянные твердых тел";
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица R.3.2.1. Некоторые постоянные твердых тел (при 20 °C). ρ - плотность; α - температурный коэффициент линейного расширения; λ - теплопроводность. |
R.3.3. Некоторые постоянные жидкостей window.top.document.title = "R.3.3. Некоторые постоянные жидкостей";
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица R.3.3.1. Некоторые постоянные жидкостей (при давлении 760 мм рт. ст.) σ – коэффициент поверхностного натяжения при указанной в соседнем столбце температуре (в – на границе с воздухом, п – на границе с парами этой же жидкости); η – вязкость при 20 °C; λ – теплопроводность при 0 °C. |
R.3.4. Некоторые постоянные жидкостей window.top.document.title = "R.3.4. Некоторые постоянные жидкостей";
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Таблица R.3.4.1. Некоторые постоянные жидкостей. ρ – плотность при 20 °C; tпл и tкип – температуры плавления и кипения при нормальном давлении; tкр – критическая температура; Pкр – критическое давление; c – удельная теплоемкость при 20 °C; q и r – удельная теплота плавления и парообразования; β – температурный коэффициент объемного расширения при 20 °C. |
R.3.5. Скорость звука в различных средах window.top.document.title = "R.3.5. Скорость звука в различных средах";
Поиск по сайту: