 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Do False
|
Читайте также: |



 "оператор" Until
"оператор" Until
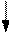
True
В цикле While... "оператор" выполняется если условие верно (True), если условие ложно (False), то цикл заканчивается, т. е. цикл While... повторяется пока выполняется условие. Цикл While... начинается проверкой условия, поэтому, если начальное условие ложно, то "оператор" не выполняется ни разу. Для включения в тело цикла нескольких операторов применяется составной оператор: Begin "операторы" end.
Цикл Repeat... повторяется, если условие ложно (False), и заканчивается, если условие верно (True), т. е. цикл Repeat... повторяется до выполнения условия. Цикл Repeat... заканчивается проверкой условия, поэтому "операторы" выполняются не менее одного раза. В теле цикла может записываться более одного оператора.
Циклы с условием обычно используются в тех случаях, если количество повторений блока операторов заранее не известно, например, при расчете суммы членов бесконечного ряда с заданной погрешностью.
Сумма членов бесконечной последовательности a1, a2, a3,..., aN,... называется бесконечным рядом и записывается в виде:
a1 + a2 + a3 +... + aN+....
Здесь aN - общий член ряда. Сумма конечного числа членов ряда называется частичной суммой и обозначается " SN ". Если сумма членов бесконечного ряда имеет конечный
предел "S", то ряд называется сходящимся. Для некоторых рядов получены формулы расчета суммы членов ряда. Например, сумма членов числового ряда:
1 + 1/32 + 1/52 +... + 1/(2*N-1)2 +... имеет предел S = Pi2/8;
и общий член aN= 1/(2*N-1)2, где N = 1, 2, 3,...
Для сходящегося ряда вычисляется последовательность частичных сумм с заданной погрешностью. Абсолютная погрешность расчетов определяется по формуле Eps=abs(S-SN), либо Eps=abs(aN), если значение S неизвестно. Относительная погрешность расчетов определяется по формуле Eps_o=abs((S-SN)/S), либо Eps_o=abs(aN/SN). Частичные суммы вычисляются по формуле: SN = SN-1 + aN;
Для знакопеременного ряда следует добавить k1=-1, а в цикле: k1:=-k1, aN=k1*aN. В некоторых случаях "N"-ый член ряда выражается через "N-1"-ый, например, для ряда:
1 + 1/2! + 1/4! + 1/6! +... + 1/(2*N)! +...; N = 0, 1, 2,...
общий член ряда вычисляется по формуле: aN = aN-1*k;
Параметр k = aN/aN-1; - коэффициент роста вычисляется предварительно (до написания программы). Для данного ряда
aN = 1/(2* N)! = 1/(1*2*... *(2*N-2)*(2*N-1)*2*N);
aN-1 = 1/(2*(N-1))!= 1/((2*N-2))!= 1/(1*2*... *(2*N-2));
k = aN/aN-1 = 1/((2*N-1)*2*N).
Здесь N! = 1*2*3*... *N; - вычисление факториала числа "N", причем 0! = 1.
Расчет частичных сумм производится в цикле с условием, например, для данного ряда операторами:
N:= 0; a:= 1; SN:= 1; e:= 2. 7182828; S:= (e2 + 1)/e;
repeat N:= N+1; k:= 1/((2*N-1)*2*N); a:= a*k;
SN:= SN+a;
Writeln('Частичная сумма Sn=', Sn:-11:6, '_ _ n=', n:2);
until abs(S-Sn) < eps; { eps - допустимая погрешность расчетов}
Writeln('_ _ _ Сумма ряда S =', S:-11:6);
Поиск по сайту: