 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Практическое задание N 2. 13
|
Читайте также: |
1. Построить траекторию движения спутника при R0=2*Rz, изменяя "e": 0 <e< 1 с шагом 0. 25, (0 <=fi<= 2*Pi). Rz=6370000, м, g=9. 81, м/с2
2. Построить траекторию движения спутника при R0=Rz изменяя "e": 1 <=e<= 2 с шагом 0. 25, (-0. 85*Pi/ Ö e <=fi<= 0. 85*Pi/ Ö e.
Примечание к п. п. 1, 2: вывести на экран начальную скорость спутника V0 и сравнить с первой космической W1=Rz* Ö(g/R0); и со второй космической W2=W1*Ö2.
Рассмотрим уравнения, описывающие прямолинейные колебания точки около неподвижного центра.
Свободные колебания точки происходящие под действием сил упругости без учета сопротивления среды называются гармоническими и описываются уравнением:


 /
/


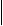


 X = A * sin(k*t + fi); / |/\/\/\/\/\/\/\| X
X = A * sin(k*t + fi); / |/\/\/\/\/\/\/\| X
/ 0
/
где X - координата точки, отсчитываемая от положения равновесия,
A - амплитуда, k - круговая частота, fi - начальная фаза колебаний.
t - параметр времени. Период колебаний tn = 2*Pi/k;
A = Ö(X02 + V02/k2); tg(fi) = k*X0/V0; k = Ö(C/M)
где X0, V0 - начальные координаты и скорость точки при t=0,
C - жесткость пружины, M - масса точки.
В случае действия небольшой силы сопротивления, пропорциональной скорости движения точки, колебания называются затухающими и описываются уравнением:
X = A1 * e(-n*t) * sin(k1*t + fi1); при n < k;
где A1 = Ö(X02 + ((V0+n*X0)/k1)2); tg(fi1) = k1*X0/(V0+n*X0);
k1 = Ö(k2 -n2); n=0.5*kc/M; kc - коэффициент сопротивления среды.
В случае действия на точку, совершающую колебания без сил сопротивления, гармонической возмущающей силы "F" с круговой частотой "p" колебания точки описываются уравнением:
X = A * sin(k*t+fi) + h/(k2-p2) * sin(p*t); при p<>k.
При p=k (явление резонанса) уравнение движения точки имеет вид:
X = A * sin(k*t+fi) - h*t/(2*k) * cos(k*t); при p=k.
В случае действия на точку, совершающую колебания, сил сопротивления и гармонической возмущающей силы с круговой частотой "p" колебания точки описываются уравнением:
X = A1 * e(-n*t) * sin(k1*t+fi1) + B1 * sin(p*t+u);
где B1 = h/Ö(k14 + 4*n2*p2); tg(u) = -2*n*p/k12; h=F/M;
Поиск по сайту: