АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Методы расчета коэффициента корреляции, их значение и практическое применение

Читайте также:
  1. B) наиболее часто встречающееся значение признака в данном ряду
  2. I и II ополчения: их состав, значение.
  3. I. Понятие и значение охраны труда
  4. II. Методы непрямого остеосинтеза.
  5. IV. Современные методы синтеза неорганических материалов с заданной структурой
  6. V. Grammatik. Wiederholen Sie die Grammatik zum Thema « Словообразование. Значение суффиксов »
  7. Write ('Значение В-',В)
  8. XX съезд КПСС. Процесс политической реабилитации и десталинизации во второй половине 1950 – начале 1960-х гг. и его значение.
  9. А) исходное расположение; б) назначение позиционного допуска; в) указание предельных отклонений размеров, координирующих оси отверстий
  10. А) Спектр света и значение разного типа излучений
  11. А. Механические методы
  12. А.) Значение Психической Энергии

При корреляционной связи одной и той же величине одного признака соответствуют разные величины другого. Например: между ростом и весом имеется корреляционная связь, между заболеваемостью злокачественными новообразованиямии возрастом и т.д.

Существует 2 метода вычисления коэффициента корреляции: метод квадратов(Пирсона), метод рангов (Спирмена).

Наиболее точным является метод квадратов (Пирсона), при котором коэффициент корреляции определяется по формул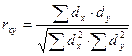е: , где

rху ― коэффициент корреляции между статистическим рядом X и Y.

dх ― отклонение каждого из чисел статистического ряда X от своей средней арифметической.

dу ― отклонение каждого из чисел статистического ряда Y от своей средней арифметической.

В зависимости от силы связи и ее направления коэффициент корреляции может находиться в пределах от 0 до 1 (-1). Коэффициент корреляции, равный 0, говорит о полном отсутствии связи. Чем ближе уровень коэффициента корреляции к 1 или (-1), тем соответственно больше, теснее измеряемая им прямая или обратная связь. При коэффициенте корреляции равном 1 или (-1) связь полная, функциональная.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)