Критерии параметрического метода оценки и способы их расчета (ошибка, репрезентативности средних и относительных величин, доверительные границы средних и относительных величин)

Любое подмножество объектов генеральной совокупности называют

выборочной совокупностью, или выборкой. Суть выборки состоит в том, что она,

являясь частью генеральной совокупности, в определенной мере может

характеризовать саму генеральную совокупность, т.е., обследуя часть объектов,

можно сделать выводы обо всем их множестве. Как правило, генеральная

совокупность имеет достаточно большое, а в идеале и бесконечное, количество

элементов. Понятно, что чем больше объем выборки, тем лучше она

представляет генеральную совокупность. Однако обследование больших

выборок или проведение сплошных обследований зачастую просто

невозможно или экономически нецелесообразно.

Реально на практике репрезентативность (представительность, типичность)

выборки обеспечивается способом отбора значений. Отбор должен гарантировать

каждому возможному значению равные шансы быть выбранным, и тогда

появление или не появление конкретного значения определяется его

частотой в генеральной совокупности, т.е. вероятностью появления тех или

иных значений.

Вероятность случайного события А ― это отношение количества элементарных

событий, благоприятствующих А к общему количеству элементарных событий.

Оценка достоверности результатов исследования базируется на теоретических

основах вероятности. Оценить достоверность результатов исследования

означает определить, с какой вероятностью возможно перенести результаты,

полученные на выборочной совокупности, на всю генеральную совокупность.

В большинстве медицинских исследований врачу приходится, как правило,

иметь дело с частью изучаемого явления, а выводы по результатам такого

исследования переносить на все явление в целом ― на генеральную совокупность.

Таким образом, оценка достоверности необходима для того, чтобы по

части явления можно было бы судить о явлении в целом, о его закономерностях.

Как бы тщательно ни производилась выборка, какой репрезентативной

ни была бы выборочная совокупность (отобранная часть наблюдений), она

неизбежно в какой-то мере будет отличаться от генеральной (общей,

исчерпывающей) совокупности. Однако в нашем распоряжении

имеются методы определения степени различий числовых характеристик

обеих совокупностей и пределов возможных колебаний выборочных

показателей при данном числе наблюдений. Как будет видно из последующего,

число наблюдений играет при этом значительную роль: чем оно больше,

тем точнее отображаются в выборке свойства генеральной совокупности и

тем меньше размеры ошибки выборочных показателей.

Теория выборочного метода, наряду с обеспечением репрезентативности

выборочных показателей, практически сводится к оценке расхождений между

числовыми характеристиками генеральной и выборочной совокупностей,

т.е. к определению средних ошибок (ошибок репрезентативности).

Эти ошибки неизбежны, так как они проистекают из сущности выборочного

исследования. Генеральная совокупность может быть охарактеризована по

выборочной совокупности только с некоторой погрешностью, измеряемой

ошибкой репрезентативности. Ошибки репрезентативности нельзя смешивать

с обычным представлением об ошибках ― методических, точности

измерения, арифметических и др.

По величине ошибки репрезентативности определяют, насколько результаты,

полученные при выборочном наблюдении, отличаются от результатов, которые

могли бы быть получены при проведении сплошного исследования всех без

исключения элементов генеральной совокупности. Это единственный вид

ошибок, учитываемых статистическими методами, которые не могут быть устранены,

если не осуществлен переход на сплошное изучение. Каждая средняя

величина ― М (средняя длительность лечения, средний рост, средняя масса тела,

средний уровень белка крови и др.), а также каждая относительная величина ― Р

(уровень летальности, заболеваемости и др.) должны быть представлены со своей

средней ошибкой ― т.

На размеры средней ошибки влияет не только число наблюдений, но

и степень колеблемости, изменчивости признака. Это совершенно очевидно

из формулы, по которой определяется средняя ошибка средней

величины (обозначаемая обычно буквой т):

где n ― число наблюдений.

Между размерами среднего квадратического отклонения (отражающего

колеблемость явления) и размерами средней ошибки существует прямая связь;

между числом наблюдений и величиной средней ошибки существует

зависимость, обратная квадратному корню из числа наблюдений.

Относительные величины (Р), полученные при выборочном исследовании,

также имеют свою ошибку репрезентативности, которая называется средней

ошибкой относительной величины и обозначается т_р. Для определения средней

ошибки относительной величины используется следующая формула:

,

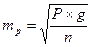где Р ― показатель, относительная величина, q ― разность между основанием

показателя и самим показателем: так, если показатель выражен в процентах,

то q = 100 – Р, если Р ― в промилле, то q – 1000 - Р, если Р ― в продецимилле,

то q = 10000 – Р и т.д.; п ― число наблюдений. При числе наблюдений менее 30

в качестве знаменателя следует взять п – 1.

Определяя для средней арифметической (или относительной) величины два

крайних значения (минимально возможное и максимально возможное), находят

пределы, в которых может быть искомая величина генерального параметра.

Эти пределы называют доверительными границами.

Доверительные границы ― границы средних (или относительных) величин,

выход за пределы которых вследствие случайных колебаний имеет

незначительную вероятность. Доверительные границы средней

арифметической в генеральной совокупности определяют по формуле:

М_ген = М_выб ± tm_м.

Доверительные границы относительной величины в генеральной совокупности

определяют по формуле: Р_ген = Р_вы6 ± tm_р,

где М_ген и Р_ген – значения средней и относительной величин, полученных

для генеральной совокупности; М_вы6 и Р_вы6 ― значения средней и относительной

величин, полученных для выборочной совокупности; m _м m _р ― ошибки

репрезентативности выборочных величин; t ― доверительный критерий.

При определении доверительных границ сначала надо решить вопрос о том,

с какой степенью вероятности безошибочного прогноза необходимо

представить доверительные границы средней или относительной величины.

Для большинства медико-биологических и медико-социальных исследований

достаточна вероятность безошибочного прогноза р = 95 % и более. Избрав такую

степень вероятности, соответственно находят величину доверительного

критерия (по специальной таблице). Таким образом, доверительный

критерий t устанавливается заранее, при планировании исследования.

Доверительные границы средней величины, вычисленные исходя из

доверительной вероятности 0,95, составляют М ± 2 т. Это означает, что

в 95 из 100 аналогичных выборок значение М будет находиться в указанных

пределах (или на 95% случаев гарантируется нахождение в этих пределах

генеральной средней).

При необходимости получения более надежных гарантий доверительности

выборочного показателя используется доверительная вероятность 0,99 (99%),

которой соответствует коэффициент t = 2,6. Утроенная средняя ошибка

(t = 3) соответствует доверительной вероятности 0,997 (99,7%). Для получения

наиболее высокой надежности результатов исследования прибегают к

вероятности 0,999 (99,9%), соответствующей значению t = 3,3.

Чем выше требования к доверительной вероятности (соответствие выборочной

средней генеральной средней), тем шире должен быть обеспечивающий такую

вероятность интервал, называемый доверительным интервалом.

Необходимость в определении доверительного интервала возникает

при желании по материалам выборочного исследования (например,

распространенность хронических заболеваний в двух дошкольных

учреждениях) дать прогноз о распространенности изучаемого явления

(хронических заболеваний) среди всех детей, посещающих дошкольные учреждения.

Интуитивно понятно, что если исследования будут продолжены дальше,

то значение определяемого показателя несколько изменится в большую или

меньшую сторону. Границы доверительного интервала как раз и показывают,

в какой степени может измениться значение определяемого нами показателя

с принятой нами вероятностью ошибки.

При небольшом числе наблюдений для вычисления доверительных границ

с указанными доверительными вероятностями (0,95; 0,99 и 0,999) значение

коэффициента t находят по специальной таблице Стьюдента. Очевидно, что

в реальных исследованиях желательно иметь как можно меньший доверительный

интервал при достаточно высокой доверительной вероятности.

Вопрос оценки различий между такими параметрами выборки, как средние

величины, является одним из самых важных в статистике медико-

биологических исследований. Многие исследования заканчиваются ответом именно

на этот вопрос. Например, при оценке токсичности какого-либо вещества обычно

берутся две группы лабораторных животных. Подбираются животные

одинакового возраста, пола, одинакового содержания и т.п., т.е. делается все,

чтобы эти группы животных представляли собой единую, как можно более

однородную статистическую совокупность. Разница заключается только в том,

что одна из групп животных (опытная) подвергается воздействию токсичного

вещества, а другая (контрольная) ― нет. В любом случае, произошли после

воздействия токсичного вещества изменения в опытной группе или нет,

разница показателей обеих групп обязательно будет иметь место. Вопрос

состоит в том, являются ли этот факт только следствием различий,

существующих в группах даже при их выборке из одной генеральной совокупности,

или разница возникла из-за того, что произошли существенные сдвиги

физиологических функций животных опытной группы. Иначе говоря,

принадлежат ли животные опытной и контрольной групп к той же самой

генеральной совокупности или опытная группа принадлежит к другой

генеральной совокупности (совокупности с измененными

физиологическими параметрами)?

Достоверность различия двух выборочных величин можно оценить

с помощью доверительных границ. Если доверительные границы одной из

этих величин не совпадают с доверительными границами другой величины,

то различие между ними следует считать статистически значимым,

существенным с тем уровнем вероятности, при котором были вычислены

доверительные границы. Если доверительные границы одного показателя

полностью или на большом протяжении совпадают с доверительными

границами другого показателя, то различие между ними признается

статистически не значимым, не существенным.

В тех случаях, когда при сопоставлении доверительных границ

трудно сделать определенное заключение о наличии или отсутствии

существенных различий между средними величинами, следует прибегнуть

к вычислению критерия значимости Стьюдента t по формуле:

,

где М₁, и М₂ — сравниваемые средние, т ₁² и, т ₂² квадраты их средних ошибок.

При вычислении t целесообразно в качестве М₁ брать большую среднюю.

Если вычисленное значение t окажется меньше 2, то различие между

средними признается случайным, статистически не значимым;

при t > 2 это различие можно считать значимым с вероятностью > 0,95;

(р < 0,05); при t > 2,6 ― значимым с вероятностью > 0,99 (р < 0,01)

и при t > 3,3 ― с вероятностью > 0,999 (р < 0,001).

При оценке достоверности относительных величин (статистических

коэффициентов) средняя ошибка вычисляется по формуле:

,

где р ― величина коэффициента в %; q ― дополнение его до 100 (100- р),

п ― общее число наблюдений.

Так же как и средняя ошибка средней арифметической, средняя ошибка

выборочного статистического коэффициента прямо пропорциональна колеблемости

этого показателя (рq) и обратно пропорциональна числу наблюдений (п).

Средние ошибки статистических коэффициентов используются для

вычисления доверительных границ последних по формуле: р ± tт,

где р ― величина статистического коэффициента; t – доверительный

коэффициент, соответствующий избранной вероятности;

т – средняя ошибка статистического коэффициента. С помощью

средних ошибок вычисляется критерий Стьюдента t для оценки значимости

различия двух статистических коэффициентов:

.

Следует отметить, что значимость различий средних в малых выборках

и относительных показателей, величина которых приближается к 0 или 100 %,

оценивается с помощью специальных методов непараметрической статистики.

Вариационный ряд. Виды вариационных рядов. Величины, характеризующие вариационный ряд (мода, медиана, средняя арифметическая). Методика расчета. Оценка достоверности различий средних величин.

Вариационный ряд — это статистический ряд, показывающий распределение изучаемого явления по величине какого-либо количественного признака. Например, больных по возрасту, по срокам лечения, новорожденных по весу и т.п.

Варианта — отдельные значения признака, по которому проводится группировка (обозначается V ).

Частота— число, показывающее, как часто встречается та или иная варианта (обозначается P ). Сумма всех частот показывает общее число наблюдений и обозначается n. Разность между наибольшей и наименьшей вариантой вариационного ряда называется размахом или амплитудой.

Различают вариационные ряды:

1. Прерывные (дискретные) и непрерывные.

Ряд считается непрерывным, если группировочный признак может выражаться дробными величинами (вес, рост т.п.), прерывным, если группировочный признак выражается только целым числом (дни нетрудоспособности, число ударов пульса и т.п.).

2.Простые и взвешенные.

Простой вариационный ряд представляет собой ряд, в котором количественное значение варьирующего признака встречается один раз. Во взвешенном вариационном ряду количественные значения варьирующего признака повторяются с определённой частотой.

Поиск по сайту: