Предел текучести и температура деформации при резании

Зависимость предела текучести от температуры и деформации может быть представлена в виде

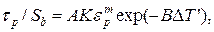(14.27)

где DT¢ – приращение гомологической температуры в зоне деформации; m, k – показатели деформационного и скоростного упрочнения; B – показатель температурного разупрочнения.

.

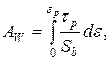
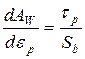Интегрируя уравнение (14.27) с учетом (14.28), получим

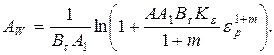(14.29)

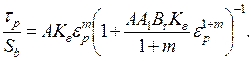(14.30)

Предел текучести достигает максимума при условии: , т. е.

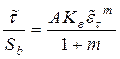при 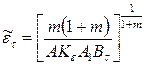. (14.31)

Максимальный предел текучести при резании сталей приблизительно в два раза больше, чем предел текучести этого же материала при статических испытаниях.

При больших скоростях, характерных для резания, тепловой поток, поступающий в деталь от условной плоскости сдвига, не зависит ни от скорости резания, ни от толщины срезаемого слоя:

Ф_д 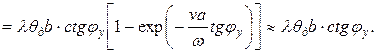(14.32)

С учетом теплового потока от плоскости сдвига в деталь температура деформации (рис. 14.10) может быть определена по формуле

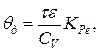(14.33)

где 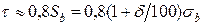, C_V = 5 МДж/м³град,

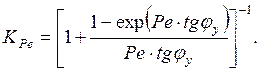(14.34)

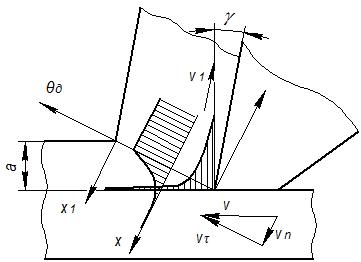
Рис. 14.10. Схема к расчету температуры деформации

При больших значениях критерия Ре, характерных для условий обработки сталей твердосплавными инструментами, .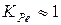

14.5. Температура полуплоскости от равномерно распределенного
быстродвижущегося источника тепла

При расчете приращения температур передней и задней поверхностей инструмента используется решение о температуре полуплоскости от равномерно распределенного быстродвижущегося источника тепла.

При увеличении критерия Пекле Ре= 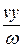изотермы температурного поля локализуются вблизи оси y и угол наклона их к этой оси уменьшается. Соответственно нормаль к изотерме, указывающая направление теплового потока и градиента температуры, составляет с осью x малый угол j_р (рис. 14.11). Вследствие этого составляющая теплового потока вдоль оси x существенно больше, чем вдоль оси y. При достаточно больших значениях критерия Ре,характерных для резания, влиянием перетоков тепла в направлении оси y на температуру, возникающую на поверхности движущейся полуплоскости, можно пренебречь.

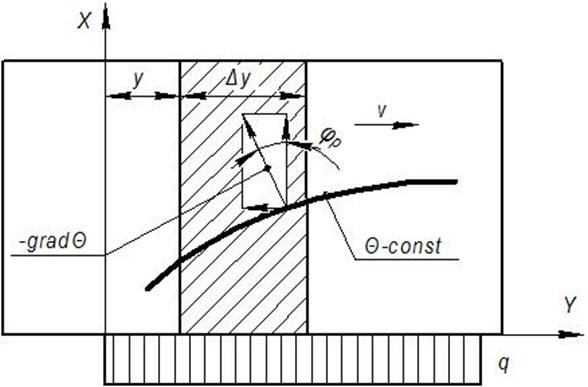
Рис. 14.11. Схема к расчету температуры в полуплоскости
от быстродвижущегося равномерно распределенного источника тепла

Пренебрегая перетоками тепла вдоль оси y, элемент полуплоскости шириной Dy можно рассматривать как теплоизолированный полуограниченный стержень, к торцу которого в течение некоторого времени

(14.35)

подводится постоянный тепловой поток плотностью q, а температурное поле полуплоскости – как совокупность независимых друг от друга одномерных нестационарных процессов в стержнях. Температура неограниченного стержня, к торцу которого подводится тепловой поток постоянной плотности, описывается решением

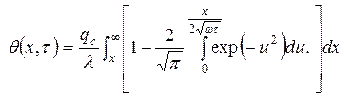. (14.36)

Из формулы (14.36) при x = 0 следует, что температура на торце стержня прямо пропорциональна плотности теплового потока, обратно пропорциональна коэффициенту аккумуляции тепла и будет повышаться с течением времени пропорционально корню квадратному от времени нагрева:

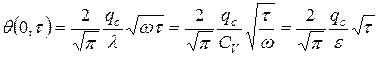, (14.37)

где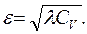

Воспользовавшись (14.36), получим

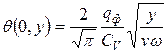. (14.38)

Как следует из (14.38), при постоянной плотности теплового потока q увеличение скорости v источника тепла приводит к уменьшению температуры.

Поиск по сайту: