Требующих применения арифметических знаний

Вопрос о том, насколько глухие дети оказываются в состоя­нии применять знания на практике, является одним из самых актуальных вопросов обучения. Арифметические знания необхо­димы человеку в трудовой деятельности и повседневной прак­тике. Арифметика нужна не только для пересчета и измерения предметов, для сравнения их по количеству, но и для решения различных задач, поставленных жизнью. При этом часто суще­ствует несколько способов решения практической задачи и нуж­но выбрать из них самый экономный, обеспечивающий быст­рое получение точного результата.

В исследовании Т. В. Розановой (1966) предлагалось глухим учащимся (V, VIII и XI классы) решать практические задачи. Например, требовалось узнать, сколько можно вырезать из желтой тесьмы бантов определенной величины (при этом давал­ся кусок тесьмы и образец банта). Как показало исследование, учащиеся пользовались тремя способами решений. В одних слу­чаях измеряли (например, отрезки тесьмы и бант) и сразу после этого записывали ответ на вопрос задачи, в других — за изме­рением отрезков следовала арифметическая запись решения и ответа и в третьих — решение осуществлялось практически (на­пример, путем сопоставления отрезков тесьмы).

Те решения, которые ограничивались измерением отрезков, были двух видов, существенно различных по внутреннему содер­жанию. В одних решениях испытуемые, измерив два отрезка тесьмы или бумаги, мысленно вычисляли, во сколько раз или на сколько сантиметров один отрезок больше другого, и после этого записывали ответ. Такие решения встретились всего у трех уча­щихся (у двух из XI класса и у одного из VIII класса), и они свидетельствовали об относительно высоком уровне развития процессов обобщения и конкретизации у этих глухих школьни­ков. Учащиеся сразу соотносили условия практической задачи с имеющимися у них арифметическими знаниями и использовали при решении лишь определенные знания, адекватные данной за­даче. Быстрота, с которой достигалось решение, без каких-либо опор во внешней деятельности (без арифметической записи и т. п.) указывала на высокую свернутость и автоматизирован-ноеть мыслительных операций у этих школьников. Еще одной чертой, характеризующей деятельность этих трех школьников, было то, что они по собственной инициативе в некоторых зада­ниях проверяли получившийся у них результат путем предмет­но-действенного сравнения отрезков. Такое обращение к прак­тической проверке результата также показатель относительно высокого уровня их мыслительной деятельности.

Решения другой группы испытуемых имели лишь внешнее сходство с только что описанными. Испытуемые измеряли оба сравниваемых отрезка или один из отрезков и, считая, что толь­ко лишь в этом и заключается задание, записывали ответ, напри­мер: «90 ам можно вырезать бантов». В этих случаях глухие учащиеся упрощенно понимали содержание заданий. Они соеди­няли внешним образом результат измерений со словами из текс­та задачи, что свидетельствовало об относительно элементар­ном уровне их мыслительной деятельности.

Отмеченные две группы решений задач глухими детьми явля­лись как бы двумя противоположными полюсами, между кото­рыми распределялись все прочие решения — измерение отрез­ков, а также записи арифметических вычислений и ответов.

Наблюдались различные виды решений с точки зрения того, какие знания применялись и как учитывались особенности пред­метной ситуации. В ряде случаев глухие дети решали задачи, ис­пользуя неправильный способ арифметических действий. Они ориентировались на отдельные слова вопроса задачи, применяя тем самым не знания, а «псездознания».

Некоторые испытуемые допустили ошибки совсем иного ро­да при решении задачи, в которой требовалось узнать, сколько бантов выйдет из тесьмы. При измерении банта они не учли, что он был' свернут, и измерили его, не развернув. В этом случае, как часто бывает в практической деятельности, можно было при­менить знания, лишь несколько изменив предметную ситуацию, что испытуемые не смогли сделать.

Очень немногие учащиеся соотносили полученный результат решения с предметной ситуацией (так делали только те, кто пользовался сокращенными способами решения в мысленном плане). Большинство же детей считало задачу решенной после написания ответа. Казалось удивительным, что почти никто из испытуемых не пытался проверить результаты своих вычислений на практике.

Испытуемых специально спрашивали, как они могли бы про­верить результат решения, как можно было бы решить задачу другим способом.

Только два испытуемых (один из V, другой из XI класса), когда их спросили об этом, сразу указали на возможный прак­тический способ решения (например, при решении одной из за­дач они говорили, что можно наложить один кусок бумаги на другой кусок, чтобы узнать, во сколько раз второй кусок бумаги длиннее первого), а затем и выполняли это практическое реше­ние. Остальные предлагали проверить решение путем новых арифметических вычислений (например, делить делимое на част­ное) или повторно измерить длину кусков бумаги.

Из этого следует, что ситуация арифметического решения задачи и практического действования с предметами оказывались для многих глухих детей изолированными друг от друга. ■ Два низших уровня применений знаний (применение «псевдо­знаний» и применение знаний без соотнесения результата ариф­метического решения с практической ситуацией) чаще наблюда­лись у глухих детей и подростков, и они почти не встречались у глухих учащихся старших классов.

Решение задач предметно-действенными способами

Решение практической задачи часто бывает возможным без применения каких-либо специальных знаний. Однако в этих слу­чаях оно может стать менее точным и потребовать относитель­но более длительного времени, чем в случае решения практиче­ской задачи с применением знаний. Так, выясняя вопрос о том, сколько бантов выйдет из тесьмы, многие глухие учащиеся раз­вертывали бант и накладывали его на вытянутую тесьму (при этом либо загибали тесьму по длине банта, складывая ее «гар­мошкой», либо отмечали на тесьме конец банта и перекладывали бант вдоль по тесьме). Иногда решение затягивалось из-за того, что лента выпадала из рук или скручивалась, терялись сделан­ные отметки и испытуемый вынужден был начинать работу сна­чала; некоторые это делали по нескольку раз. Не всегда испы­туемым удавалось достаточно точно совместить бант и тесьму, поэтому они считали, что получится на один бант больше или меньше, чем на самом деле.

Таким образом, на решение простой практической задачи затрачивалось довольно много времени, и результат получался не всегда точным, хотя способ решения задачи был избран вер­но. С возрастом у глухих детей заметно совершенствовались от­дельные приемы практических действий, что обеспечивало более быстрые и точные решения (особенно у учащихся в период от VIII к XI классу).

Иногда глухие учащиеся избирали заведомо неправильный способ практического решения. Например, чтобы решить задачу про банты, они складывали по нескольку раз ленту и приклады­вали ее к завязанному банту, пытаясь понять, сколько таких завязанных бантов содержится в сложенной ленте. Число таких решений заметно сокращалось у учащихся от VIII к XI классу (в два с половиной раза), что также свидетельствовало о разви­тии практического мышления у глухих учащихся в этот период.

Глухие дети далеко не всегда оказывались в состоянии доста­точно точно выразить в словесной речи, к какому результату они пришли на основе предметно-действенного решения задачи. На­пример, в одной из задач требовалось определить, во сколько раз один кусок бумаги длиннее другого. Испытуемые путем наложе­ния одного куска на другой правильно определяли в действии, что один кусок укладывается в другом 12 раз. Но затем некото­рые из них неправильно говорили, что получится «12 сантимет­ров» или «12 метров».

Трудности словесного выражения того результата, который был получен при практическом решении, уменьшаются у глухих детей с возрастом. Однако педагогу, обучающему глухих, необ­ходимо фиксировать на них свое внимание. Ведь если глухие де­ти ошибаются в словесном выражении каких-либо предметных отношений, то они и недостаточно ясно осмысливают эти отноше­ния или такое осмысливание совершается лишь приуроченно'к практическому действию, без должной обобщенности и система-тизированности.

Отношения между арифметическими и предметно-действенными способами при решении практических задач

Исследуя представления глухих детей о форме и количестве предметов, А. И. Дьячков (1957) показал, что эти дети часто вполне адекватно выполняли различные задания на практике, ориентируясь на определенные форму или количество предме­тов, но при специальной учебной задаче не могли сопоставить предметы по форме и количеству.

Исследование Т. В. Розановой (1966) обнаружило, что глухие дети часто не связывали арифметических решений практических задач с их решениями предметно-действенными способами. Для формирования у глухих детей внутренних связей и переходов от

предметно-действенных способов мышления к арифметическим и обратно требовался значительно больший срок обучения, чем для слышащих детей.

В исследовании Н. В. Яшковой (1964) глухие ученицы VIII и X классов, уже обучавшиеся составлению выкроек по обмерам и раскрою тканей, должны были: 1) произвести необходимые об­меры куклы, для того чтобы сшить ей кофточку без рукавов; 2) рассчитать, сколько для этого потребуется ткани; 3) выбрать из нескольких кусков ткани тот, из которого выйдет кофточка, чтобы расход ткани был минимальным.

Оказалось, что лишь немногие ученицы при расчете количест­ва требующейся ткани использовали ранее произведенные ими обмеры куклы. Полрвина этих учениц, воспользовавшись числа­ми, полученными при обмерах, выполнила арифметическое реше­ние, лишенное какого-либо практического смысла, и, естественно, получила совсем неверные результаты. При выборе же куска тка­ни учащиеся никак не использовали свое арифметическое реше­ние, а осуществляли этот выбор предметно-действенным спосо­бом (прикладывали разные куски ткани к кукле).

Таким образом, во-первых, глухие учащиеся не смогли при­менить нужные знания, чтобы правильно определить нужное количество ткани, и, во-вторых, они не использовали результаты своих арифметических вычислений (расчеты) в последующей практической деятельности, для которой эти расчеты были очень важными. Поэтому и выбор куска ткани был сделан значительно менее точно, чем если бы учащиеся могли использовать пра­вильные расчеты.

Из приведенных фактов следует, что достаточно высокий уровень практической деятельности будет обеспечен лишь при условии постоянных переходов от теоретических (в том числе арифметических) способов решения задач к предметно-действен­ным и обратно. Для этого нужно, чтобы знания применялись систематически во всех необходимых случаях, когда они могут облегчить практическое решение, сделать его более быстрым и более точным. Чтобы воспитать у детей интерес к применению знаний, когда последние у них уже достаточно прочны, необходи­мо предоставлять им возможность убеждаться в практической полезности применения знаний. Следует сопоставлять два пути решения, практический и теоретический, и показывать, что теоре­тический путь обеспечивает более точное и быстрое решение (как, например, при решении задачи, сколько можно вырезать малень­ких бантов определенной длины из длинной тесьмы). В этой свя­зи большого внимания заслуживает статья учительницы ариф­метики в школе глухих В. М. Петровой (1964), тщательно раз­работавшей систему практических и теоретических задач при изучении периметра, площади и объема.

Вместе с тем с точки зрения применения знаний бесполезны те практические работы, в которых решение легче получить прак-

тически, чем теоретическим способом (например, узнать, сколько маленьких кусков бумаги можно вырезать из полоски, в которой укладывается этот кусок всего четыре раза, и задачу можно быстро и точно решить, наложив кусок на полоску). Задачи по­добного рода с простыми и ясными отношениями между величи­нами очень важны на этапе формирования знаний, но они сов­сем неуместны на этапе их применения.

Целесообразно давать детям такие практические работы, в которых возможности применения тех или иных знаний не были бы сразу очевидны. Тогда дети, прежде чем применить знания, должны будут изменить предметную ситуацию, чтобы найти воз­можный способ теоретического решения.

Очень важно учить детей применять знания не столько в за­даниях искусственных, специально составленных педагогом, сколько в самой практической и особенно трудовой деятельно­сти. При этом практические задачи следует искать именно там, где применение знаний будет действительно полезно.

3. Особенности выполнения практических заданий зрительно-пространственного характера

Специальное исследование имело целью выявить, каковы осо­бенности мышления глухих детей и подростков при выполнении практических заданий зрительно-пространственного характера (Н. В. Яшкова, 1968). Операции анализа и синтеза, неразрывно связанные между собой в процессе любой умственной деятель­ности, имели большое значение и при решении этих задач. Свое­образие заданий состояло в том, что для их выполнения требо­валось умение переходить от предметно-действенных форм ана­лиза и синтеза объекта к мысленным и обратно.

Испытуемые должны были, руководствуясь картинкой, подо­брать и сложить из готовых деталей кукольный фартук (на кар­тинке была изображена кукла в фартуке). Набор состоял из де­талей трех фартуков разного фасона (рис. 47). При этом требо­валось выбрать детали определенной формы в нужном количест­ве и отказаться от лишних. Порядок предъявления деталей был постоянным, что обеспечивало единообразие условий опыта. Ис­пытуемым предлагали внимательно посмотреть на картинку, за­тем объясняли, что набор состоит из трех фартуков, а надо выбрать один и сложить его. При этом подчеркивалось, что надо выбрать и сложить именно такой фартук, как нарисо­ванный. В опытах участвовали глухие школьники II, IV, VI, VIII и X классов, а также слышащие ученицы IV и VI классов.

В случае затруднений при выполнении этого задания испы­туемым оказывалась помощь в словесной и наглядно-практичес­кой форме. Характер помощи был строго определенным, и тща­тельно соблюдалась установленная последовательность в ее ока­зании. Если задача была неправильно решена испытуемым,

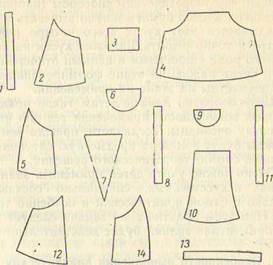
Рис. 47. Исследование мыслительной деятельности глухих детей при выполнении практических заданий. Образец и «абор деталей для составления фартука

Рис. 48. Правильное решение (а) и различные ошибки (б, в, г, д, е) при составлении фартуков

экспериментатор спрашивал его, где такой фартук, как нарисо­ванный. Это был первый этап помощи—общая стимуляция, воз­вращение ребенка к цели деятельности. Если испытуемый утвер­ждал, что сложенный им, но не соответствующий картинке фар­тук правильный, экспериментатор не соглашался с этим, повторял еще раз инструкцию, сопровождая ее жестами и соотнося опор­ные слова инструкции с картинкой. Если испытуемый и после этого продолжал утверждать, что сложенный им фартук верный, экспериментатор совсем убирал неверный фартук. Таким обра­зом, экспериментатор сначала помогал испытуемому установить словесно-наглядные соотношения, необходимые для правильного анализа картинки, а затем облегчал условия анализа, убирая часть лишних деталей, и, следовательно, делал нужные детали более заметными. Это был второй этап помощи. В тех случаях, когда и это не помогало, экспериментатор давал испытуемому набор нужных деталей фартука другого цвета, предлагал вы­брать такие же части из первого набора и сложить фартук. Та­кова была помощь третьего этапа. Глухим ученицам VIII и X класса развернутой помощи при решении не оказывали, ограни­чивались лишь общей стимуляцией и повторным разъяснением инструкции.

Правильный выбор деталей был возможен лишь на основе мысленного воссоздания конструкции фартука. Чтобы успеш-

но выполнить задание, испытуемым нужно было проявить эле­ментарные конструктивные умения.

Следует отметить, что число часов швейного дела в школе для глухих во всех классах, начиная с пятого, где оно вводится впервые, значительно больше, чем в массовой школе. Глухие уче­ницы VI класса имели преимущество в отношении подготовки по швейному делу по сравнению со слышащими девочками того же возраста. Еще более значительным было преимущество в та­кой подготовке у глухих восьмиклассниц и десятиклассниц. Вме­сте с тем это задание представляло для испытуемых собственно мыслительные трудности: требовалась мысленная обработка наглядных данных и предвидение результата на основе взаимо­действия мысленных и практических форм анализа и синтеза. Одновременно это было задание на применение определенных знаний и умений в необычных условиях, т. е. испытуемый должен был действовать мысленно и практически достаточно обобщен­ным способом.

Самостоятельно и с помощью первого вида помощи правиль­но выполнили задание около половины глухих учащихся IV и VI классов и большинство глухих учениц VIII и X классов, а также все слышащие школьницы.

Для глухих второклассников потребовалась наиболее раз­вернутая помощь при выполнении этого задания (70% случаев помощи 2-го и.3-го вида).

Практические действия с набором деталей были у глухих школьниц в ряде случаев менее рациональными, чем у слышащих девочек. Они неуверенно раскладывали все детали по отдель­ности, обращаясь к некоторым из них неоднократно, но часто так и не достигали верного решения самостоятельно или достига­ли его лишь долгим неэкономным путем. Это свидетельствует о том, что у них не возникало четкого предваряющего образа из­делия. Основные ошибки при выполнении этого задания были связаны с упрощением глухими школьницами фасона фартука, который нужно было сложить, и свидетельствовали о недоста­точно полном анализе картинки и нечеткости предваряющего об­раза фартука (рис. 48).

Характер деятельности испытуемых разного возраста при вы­полнении описанного задания позволяет утверждать, что путь формирования изучавшихся действий и мыслительных операций идет от чисто манипулятивных, предельно развернутых действий (первоначально еще не направленных на результат) через про-бовательные действия и неполное предвидение результата к пол­ному его предвидению. Постепенно действия становятся все бо­лее обобщенными, четкими и экономными, исчезают трудности мысленного оперирования наглядными данными.

Типы решений были в этих опытах одни и те же у глухих и слышащих испытуемых. Однако у глухих детей и подростков бы­ло меньше, чем у слышащих, самостоятельных решений наиболее высокого уровня, когда действия с объектами были достаточно обобщенными и выполнялись вполне уверенно, точно и эконом­но. Это свидетельствовало о четкости образного предвидения ре­зультатов действий и о полноценном включении мыслительных операций в решение практической задачи. Слышащие ученицы IV—VI классов дали около половины решений этого уровня, в то время как у глухих учеников IV, VI класса и восьмиклассниц совсем не было таких решений, а у глухих десятиклассниц их оказалось всего 28%.

В решениях следующего уровня, основанного, как и первый, на успешно совершившемся мысленном анализе картинки, дейст­вия испытуемых представляли собой более или менее разверну­тый поиск нужных деталей. Здесь предвидение результата дей­ствий имело место, но оно не было столь отчетливым, как в реше­ниях первого типа. В ходе решения дети пользовались приемами, облегчающими анализ наглядных данных, они повторно, а иног­да и неоднократно обращались к картинке, планомерно сорти­руя и сопоставляя детали фартуков. Это свидетельствовало о стремлении испытуемых уточнить свое представление о конструк­ции изделия, внести при помощи предметно-действенного анали­за некоторые поправки в результат мысленного анализа объекта.

К этому типу были отнесены не только самостоятельные ре­шения, но и с использованием помощи. Решения этого типа со­ставили около трети всех решений глухих учеников II класса и

около половины — IV, VI, VIII и X классов. Для глухих такие решения были наибольшим достижением в каждой возрастной группе (кроме десятиклассниц). Для слышащих же детей это был наиболее элементарный уровень решений (половина всех решений).

Значительно менее совершенным был третий тип решений. Испытуемые оказались не в состоянии произвести мысленный анализ фасона. Они раскладывали все детали по отдельности, иногда группируя и перегруппировывая их. Откладывали и сно­ва брали некоторые части. В ряде случаев отмечалось по несколь­ку обращений к картинке. При этом некоторые испытуемые чер­тили в воздухе основные линии фасона, глядя на картинку, или обводили эти линии по картинке, создавая себе таким образом опору при анализе. Подбор и складывание нужных деталей, осу­ществлялись неуверенно и занимали значительно больше време­ни, чем в предыдущих случаях. Испытуемые производили до 30 операций (вместо шести при первом типе решений), т. е. прак­тический анализ очень затягивался.

Эти наименее совершенные решения, несмотря на помощь экспериментатора, составили около 2/3 всех случаев во II клас­се и около половины в IV и VI классах школы глухих. В VIII классе была половина таких решений, а в X классе—около 1/4, причем ученицам этих классов помощи не оказывали. В решени­ях этого типа у глухих детей наблюдались наиболее грубые ошибки в выполнении описанного задания (например, испыту­емые сложили асимметричный фартук с одним боком или «двухъярусное» сооружение, см. рис. 48).

Эти данные заставляют обратиться к вопросу об интеллек­туальном уровне практической деятельности глухих учащихся, особенно школьниц старшего возраста, для которых предлагае­мые задания были сходны с привычной деятельностью. Освоение достаточно сложных форм мыслительной деятельности позволя­ет выполнять практические действия рациональными, наиболее экономными способами. Именно недостаточная свобода мыслен­ного оперирования пространственными образами и трудности в осуществлении единства мысленных и практических форм анали­за и синтеза были причиной того, что у глухих школьниц значи-k тельно дольше, чем у слышащих, сохранялись более элементар­ные способы выполнения практических заданий.

Поиск по сайту: