Прямая и двойственная задача

Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другого (но также линейного) типа задачу, называемую двойственной (или сопряженной) по отношению к исходной, или прямой.

Прямая ЗЛП заключается в том, чтобы найти максимум значения функции цели

(16)

при условиях ,

,

……………………………..

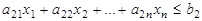, (17)

,

………………………………….

,

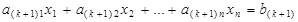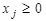_, (j=1…l, l≤ n).

О п р е д е л е н и е. Задача, состоящая в нахождении минимального значения функции

(18)

при условиях

,

,

……………………………….

, (19)

,

………………………………

,

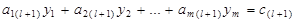, (i=1…k, k ≤ m),

называется двойственной задачей по отношению к задаче (16)-(17).

Задачи (16)-(17) и (18)-(19) образуют пару задач, называемую в линейном программировании двойственной парой.

Сравнивая две сформулированные задачи, видим, что двойственная задача по отношению к исходной составляется согласно следующим правилам.

1.Функция цели прямой задачи задается на максимум (минимум), а функция цели двойственной задачи – на минимум (максимум).

2. Матрица коэффициентов при переменных в системе ограничений прямой задачи

и аналогичная матрица в двойственной задаче

получаются друг из друга транспонированием (т.е. строки становятся столбцами, а столбцы – строками).

3. Число переменных в двойственной задаче равно числу ограничений в прямой задаче, а число ограничений в двойственной задаче – числу переменных в прямой задаче.

4. Коэффициентами при переменных в функции цели двойственной задачи являются свободные члены в системе ограничений прямой задачи, т.е. вектор B=(b₁, b₂, b₃, …, b_m), а свободными членами в ограничениях двойственной задачи становятся коэффициенты при переменных в функции цели прямой задачи, т.е. вектор С=(с₁, с₂, с₃, …, с_n).

5. а) Если переменная x_j в прямой задаче может иметь только положительное значение, то j – е ограничение в двойственной задаче является неравенством типа “ ≥ ” (в двойственной задаче не может быть ограничений –неравенств типа “ ≤ ”);

б) если переменная x_j в прямой задаче может принимать любое (в том числе и отрицательное) значение, то соответствующее ограничение (т.е. j -е) в двойственной задаче записывается в виде уравнения (равенства);

в) если i – е ограничение в прямой задаче записано в форме неравенства, то i – я переменная y_i в двойственной задаче будет принимать только положительное значение;

г) если i – е ограничение в прямой задаче записано в форме уравнения (равенства), то i – я переменная y_i в двойственной задаче может принимать любое значение.

Вышеприведенные соотношения в формировании прямой и двойственной задач в кратком виде представлены в таблице 11.

Таблица 11

Алгоритмы записи прямой и двойственной ЗЛП

Прямая задача	Двойственная задача
→ max	→ min
, X ≥ 0	, Y ≥ 0
, X - любое	, Y ≥ 0
, X ≥ 0	, Y - любое
, Х - любое	, Y - любое

Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре ограничения как в прямой, так и в двойственной задаче выражаются через неравенства (соответственно все переменные – положительные числа).

З а д а ч а 8. Для задачи, состоящей в максимизации функции

при условиях ,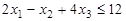

,

,

сформулировать двойственную задачу.

Р е ш е н и е. Для прямой и двойственной задач прежде всего составим матрицу коэффициентов в ограничениях:

, .

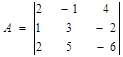В соответствии с общими правилами задача, двойственная по отношению к прямой, формулируется следующим образом: найти минимум функции при условиях

,

,

,

.

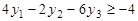Заметим, что в записанной двойственной задаче переменная y₂ может принимать любое значение, так как второе ограничение прямой задачи - равенство.

Поиск по сайту: