Решение задач условной оптимизации методом Лагранжа

Одним из наиболее общих подходов к решению задачи поиска локального минимума или максимума функции при наличии ограничений на ее переменные (задача условной оптимизации) является метод Лагранжа. Он относится к непрямым методам оптимизации. Сущность метода заключается в следующем.

Пусть функция цели задана в виде уравнения

,

а на переменные заданы ограничения

, (i=1…m),

причем на переменные не наложены условия неотрицательности. Ограничения, заданные в виде уравнений (равенств), свидетельствуют о том, что ОДР – это линия пересечения поверхности отклика функции цели и поверхностей отклика ограничений.

Взамен поиска условного максимума (минимума) вводится так называемая функция Лагранжа, для которой рассматривается безусловная оптимизация: , (28)

где λ_i – множители Лагранжа.

Функция (28) называется “Лагранжиан”. Он имеет (n+m) неизвестных. Очевидно, что входящая в его структуру сумма должна быть равна нулю. Поэтому исходная функция цели и Лагранжиан будут иметь общие стационарные точки (экстремумы). Для поиска максимума (минимума) Лагранжиана находят частные производные и приравнивают их нулю:

, (j=1…n);

, (i=1…m).

Получена система, включающая (n+m) уравнений с таким же количеством неизвестных . Всякое ее решение определяет точку , в которой может быть экстремум функции . Следовательно, решив систему уравнений, получают все точки, в которых функция цели (а более точно - линия пересечения двух поверхностей) может иметь экстремальное значение. В дальнейшем, применяя классические подходы математического анализа, исследуют эти точки на тип экстремума.

Итак, определение экстремальных точек задачи нелинейного программирования методом множителей Лагранжа включает следующие этапы:

- составляют функцию Лагранжа (Лагранжиан);

- находят частные производные от функции Лагранжа по переменным х_j

и λ_i и приравнивают их нулю;

- решая систему (n+m) уравнений частных производных, находят точки,

в которых целевая функция может иметь экстремум;

- среди точек, подозрительных на экстремум, находят такие, в которых

достигается заданный экстремум, и вычисляют значение функции цели

в этих точках.

З а д а ч а 27. По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть получены по двум технологиям. По первой технологии расходы для изготовления х₁ объема продукции издержки составят 4х₁+х₁² руб, для х₂ составят 8х₂+х₂² руб. Найти объемы производства изделий по первой и по второй технологии при условии, что суммарные издержки будут минимальными.

Р е ш е н и е. Математически условие задачи записывается следующим образом: найти минимум функции

при ограничении ,

.

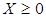Сначала найдем решение, пользуясь геометрическим методом, описанным выше. Для этого, применив элементарные преобразования, перепишем функцию цели следующим образом:

.

Очевидно, что линии уровней функции цели будут представлять набор окружностей с центром в точке с координатами (-2;-4), а область допустимых решений – линия АВ, рис. 20.

Решением задачи будут координаты точки D, которая является точкой касания линии ограничений и окружности – линии уровня (функции цели). Их можно найти следующим образом. Рассматривая функцию цели как неявную

функцию, найдем ее производную:

,

Рис.20. Геометрическая интерпретация задачи 27

откуда запишем .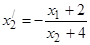

Так как уравнение линии ограничений АВ имеет вид

,

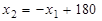т.е. это прямая, угловой коэффициент которой k= -1, запишем:

или .

Совместно с уравнением функции цели запишем систему:

,

,

решением которой будут координаты точки D, а соответственно оптимальный план задачи: ; ; руб.

Теперь решим задачу, используя метод множителей Лагранжа. Заметим, что рассматриваемая задача будет иметь геометрическую трактовку, представленную на рис.19, с той лишь разницей, что центр параболоида - поверхности отклика функции цели имеет координатное смещение , . Итак, ищем минимальное значение функции цели при ограничительном условии. Для этого составим функцию Лагранжа:

,

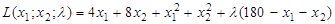вычислим ее частные производные по х₁, х₂, λ и приравняем их нулю:

,

,

.

Перенося λ в первых двух уравнениях в правую часть и приравнивая их левые части, получим:

,

или .

Решая последнее уравнение совместно с уравнением ограничений, находим: ; . Это координаты точки D в проекцияхна горизонтальные оси. Эта точка является подозрительной на экстремум. Используя вторые производные, получаем:

,

,

следовательно, в точке D имеем минимум. Этот результат и был получен выше.

Поиск по сайту: