Программирования. Появление нелинейных уравнений (или неравенств) в постановке задачи оптимизации значительно усложняют решение

Появление нелинейных уравнений (или неравенств) в постановке задачи оптимизации значительно усложняют решение. Прежде всего уже из рассмотренных выше задач очевидны некоторые свойства ЗНП, отражающие их специфику. Например:

- область допустимых решений может иметь очень сложную структуру;

- максимум функции цели (или минимум) может достигаться как

внутри ОДР, так и на ее границах;

- в задачах нелинейного программирования метод нахождения решения

зависит от вида задания ограничений (равно как их наличие или

отсутствие).

С целью пояснения ряда перечисленных проблем воспользуемся методами математического анализа из области исследования функций и рассмотрим некоторые особенности решения экстремальных нелинейных задач.

Предположим, имеются три заметно отличающихся по виду нелинейные функции ; ; 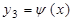, графики которых на заданном отрезке принимают вид, представленный на рис. 18.

Если, например, оптимизационная задача не имеет ограничений, то для функций y₁ и y₂ объективно существует экстремум (точки А и В соответственно) и такие экстремумы носят название глобальных максимумов (минимумов). Для функции y₃ его не существует. Однако и такого типа функции с

Рис.18. Виды экстремумов в задачах нелинейного программирования

полным правом также могут рассматриваться как подлежащие оптимизации, но при этом обязательно наличие ограничений, накладываемых на переменные. При этом для таких функций следует говорить не о стационарных точках, а о точках максимального (минимального) значения функции. Например, если имеется ограничение , то для функций y₁ и y₂ экстремум будет совпадать с глобальным экстремумом, а для функции y₃ это точка С, которая в таком случае называется локальным максимумом или условным экстремумом. Отметим, что таковой существует только при наличии ограничений. Но в ЗНП встречаются случаи, когда ограничениями являются уравнения, т.е. равенства. Рассмотрим более подробно такую ситуацию.

Ранее рассматриваемые задачи, решаемые с помощью графических построений, как уже отмечалось, представлялись в двухкоординатной системе. Такой метод обладает высокой информативностью и наглядностью для линейных задач. Однако для нелинейных задач применение геометрических методов зачастую крайне затруднено. Тем не менее, попробуем воспользоваться этим методом для рассмотрения сути постановки и метода решения оптимизационной задачи нелинейного типа.

Рассмотрим следующую задачу. Функция цели имеет вид:

.

Найти ее минимальное значение при двух видах ограничений:

а) ;

б) .

Для более наглядного представления о задаче рассмотрим ее геометрическую трактовку. С этой целью функцию цели будем рассматривать как уравнение в трех координатах – х₁; х₂; F. Очевидно, что в таком случае она будет представлена поверхностью параболоида вращения (рис. 19). Тогда линии уровней – это окружности, которые являются следами пересечения поверхности отклика функции цели с горизонтальными плоскостями на высоте F и проектируемыми на плоскость х₁0х₂ (см. задачу 27).

Рис.19. К обоснованию методики нахождения оптимума нелинейной функции

Ограничение в такой интерпретации – это уравнение плоскости, заданное в отрезках на осях, т.е. это вертикальная плоскость , отсекающая на осях Ох₁ и Ох₂ отрезки по отметкам х₁=a; х₂=b. По условию ограничение может быть задано в виде уравнения (равенства) или в виде неравенства. В первом случае ограничение – плоскость, которая при пересечении с поверхностью параболоида (т.е. поверхностью функции цели) дает кривую S. Теперь, если ограничение – это равенство, т.е. уравнение, то решение задачи следует искать на пересечении поверхностей, описываемых двумя функциями – функцией цели и функцией ограничений. Это кривая S, которая в данном случае и представляет “область” допустимых решений. Тогда речь может идти только о минимуме и ему будет соответствовать точка D, координаты которой на оси Ох₁ и Ох₂ будут оптимальным планом, а ее проекция на ось OF – оптимальным значением функции цели.

Если ограничение – неравенство, например, вида, приведенного выше, то решение следует искать уже на поверхности параболоида, отсеченной плоскостью ограничений и имеющей координаты х₁<a, x₂<b. В данном случае это будет вершина параболоида. Но так как она находится в начале координат (по структуре уравнения функции цели), то и решение будет следующим: , . Это глобальный минимум для параболоида. Поэтому, решая задачу нелинейного программирования, всегда надо достаточно детально представлять себе возможную геометрическую трактовку задачи.

Решение экстремальных задач возможно различными методами. Прямыми являются классические методы математического анализа, где они достаточно подробно рассмотрены. Непрямые методы требуют нахождения вспомогательной функции, исследование которой дает решение задачи. При этом решение может быть найдено в результате однократного вычислительного процесса (см. ниже метод Лагранжа) или в виде многократного итерационного процесса (динамическое программирование).

Глобальным называется экстремум, который ищется в условиях отсутствия ограничений. При его поиске возможна ситуация, когда его может не быть вообще, либо он является локальным экстремумом.

Условный экстремум ищется только при наличии ограничений. В связи с таким разнообразием условий методы нелинейного программирования очень детерменированы. Как уже отмечалось выше, наиболее детально разработаны методы решения ЗНП, в которых функции цели и ограничений заданы в квадратурах, т.е. показатели степени не выше двух. Мы также в настоящем курсе не будем выходить за рамки квадратурных функций.

Поиск по сайту: