Программирования

Градиентные методы относятся к прямым методам нахождения экстремума. Кроме того, они применяются как при наличии ограничения, так и при их отсутствии. Все градиентные методы – итерационные. Процесс нахождения решения задачи с помощью градиентных методов состоит в том, что, начиная с некоторой точки Х^(к), осуществляется последовательный переход к некоторым другим точкам до тех пор, пока не выявляется приемлемое решение исходной задачи.

Очевидно, что при таком подходе важны следующие обстоятельства:

- выбор первоначальной точки отсчета;

- направление, в котором следует перемещаться в ходе реализации

последовательного перемещения по опорным точкам;

- скорость перемещения исследуемой точки в заданном направлении;

- результат будет иметь приближенное значение с наперед заданной

точностью.

Кроме того, к этому процессу добавляется наличие и вид области допустимых решений, т.е. каким образом итерационный процесс должен учитывать наличие или отсутствие ОДР. В связи с этим градиентные методы могут быть подразделены на две группы.

К первой группе относятся методы, при использовании которых исследуемые точки не выходят за пределы ОДР. Наиболее распространенным из таких методов при наличии ограничений является метод Франка-Вульфа.

Ко второй группе относятся методы, при использовании которых исследуемые точки могут как принадлежать, так и не принадлежать (временно) ОДР. Однако в результате итерационного процесса в конечном итоге находится точка ОДР, определяющая приемлемое решение. Из таких методов наиболее часто используется метод штрафных функций или метод Эрроу-Гурвица.

При нахождении решения ЗНП градиентными методами итерационный процесс осуществляют до того момента, пока градиент функции в очередной точке Х^(к+1) не станет равным нулю или же пока , где ε – достаточно малое положительное число, характеризующее точность полученного решения.

Общим в рассматриваемых методах является понятие о градиенте функции. Если имеется функция 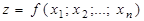и каждой переменной, входящей в данную функцию, дано приращение Δ х=dx (т.е. приращение аргумента всегда равно его дифференциалу), то очевидно, что функция также будет иметь приращение, определяемое из равенства:

.

Пользуясь правилами векторной алгебры, запишем:

,

где вектор-строка

носит название градиента функции z.

Градиент функции – вектор-строка, элементы которой состоят из частных производных функции, т.е. тангенсов углов касательных, проведенных к поверхности отклика в плоскости, параллельной данной оси.

Интегрально это обобщенная величина направления, по которому функция изменяется наиболее динамично.

Поиск по сайту: