 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Математическая постановка задачи
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления (склады) в n пунктов назначения (потребители). При этом в качестве критерия оптимальности обычно принимается минимальная суммарная стоимость перевозок всего запаса грузов ко всем потребителям (либо минимальное время его доставки). Рассмотрим первый вид постановки задачи.
Обозначим через cij тарифы перевозки единицы груза из i – го пункта отправления в j – й пункт назначения (рис. 9 а), через ai – запасы груза в i – ом пункте отправления, через bj - потребность в грузе в j – ом пункте назначения, а через xij – количество единиц груза, перевозимого из i – го пункта отправления в j – й пункт назначения (рис. 9b).

Рис.9. К обоснованию математической модели транспортной задачи
Тогда математическая постановка задачи состоит в определении минимального значения функции
 или
или  → min (i=1…m; j=1…n) (20)
→ min (i=1…m; j=1…n) (20)
при условиях  ,
,
 ,
,
……………………………

или 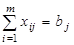 (j=1…n), (21)
(j=1…n), (21)
а также  ,
,
 ,
,
…………………………..
 ,
,
или  , (i=1…m), (22)
, (i=1…m), (22)
 .
.
О п р е д е л е н и е 1. Всякое неотрицательное решение систем линейных уравнений (21) и (22), определяемое матрицей 
 (i=1…m; j=1…n), называется планом транспортной задачи.
(i=1…m; j=1…n), называется планом транспортной задачи.
О п р е д е л е н и е 2. План  (i=1…m; j=1…n), при котором функция (20) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
(i=1…m; j=1…n), при котором функция (20) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
Обычно исходные данные транспортной задачи записывают в табличной форме (табл.15).
Таблица 15
Форма записи условий транспортной задачи
| Поставщик | Объемы поставок и тарифы по потребителям | Запасы | |||||
| В1 | В2 | ……. | Вj | …… | Вn | ||
| А1 | c11 x11 | c12 x12 | ……. | c1j x1j | ……. | c1n x1n | a1 |
| А2 | c21 x21 | c22 x22 | ……. | c2j x2j | ……. | c2n x2n | a2 |
| ……… | ……. | ……. | ……. | ……. | …….. | ……. | ……. |
| Аi | ci1 xi1 | ci2 xi2 | ……. | cij xij | ……. | cin xin | ai |
| ……… | ……. | ……. | ……. | ……. | ……. | ……. | ……. |
| Аm | cm1 xm1 | cm2 xm2 | ……. | cmj xmj | ……. | cmn xmn | am |
| Потребность | b1 | b2 | …… | bj | ……. | bn | Σ |
Очевидно, общее наличие груза у поставщиков равно  , а общая потребность в грузе у потребителя равно
, а общая потребность в грузе у потребителя равно  единиц. Если общая потребность в грузе равна запасу груза у поставщиков, т.е.
единиц. Если общая потребность в грузе равна запасу груза у поставщиков, т.е.
 , (23)
, (23)
то такая модель транспортной задачи называется закрытой или сбалансированной. Если это условие не выполняется, то такая модель называется открытой моделью транспортной задачи.
Т е о р е м а. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т.е. выполнялось равенство (23).
В случае, если запас превышает потребность, т.е. 
 ,
,
то вводится фиктивный (n+1) –й пункт назначения с потребностью

а соответствующие тарифы считаются равными нулю сin+1=0 (i=1…m). Аналогично, если запасы меньше потребностей, вводится фиктивный (m+1) –й пункт отправления с запасом груза
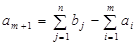
и тарифы полагаются равными нулю cm+1=0 (j=1…n). Так открытая задача сводится к закрытой транспортной задаче.
Как и в производстенной ЗЛП, в транспортной задаче существует множество опорных планов и один из них - оптимальный.
Решение транспортной задачи имеет свои особенности:
- решение задачи начинают с нахождения одного из опорных планов; его
нахождение – самостоятельная проблемная задача (см. ниже);
- план должен быть оценен на предмет подтверждения его оптимальности;
- количество базисных (ненулевых) переменных в опорном плане должно
быть равно (n+m-1). Такой план называется невырожденным. Если их
меньше, то такой план называется вырожденным и оптимизации не под-
лежит, или его надо преобразовать в невырожденный (см. ниже).
6.2. Нахождение опорного плана транспортной задачи
Как и при решении ЗЛП по планированию симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана. Рассмотрим несколько методов нахождения такого плана.
Метод северо-западного угла. На примере конкретной задачи продемонстрируем этот метод нахождения опорного плана.
З а д а ч а 12. На три базы А1, А2, А3 поступил однородный груз в количествах, соответственно равных 140, 180, 160 ед. Этот груз требуется перевезти в пять пунктов назначения В1, В2, В3, В4, В5 соответственно в количествах 60, 70, 120, 130, 100 ед. Тарифы перевозок единичного количества груза с каждого из складов в соответствующие пункты назначения указаны в табл.16. Найти план перевозок данной транспортной задачи методом северо-западного угла.
Таблица 16
Структурная запись задачи
| Поставщик | Пункт назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребность |
Р е ш е н и е. Введем понятие маршрута – наименование клетки АiBj, где i – порядковый номер поставщика, j – порядковый номер потребителя.
Задача является закрытой, так как количество имеющегося у поставщиков грузов равно объему грузов, запрашиваемых потребителями. Здесь число пунктов отправления m=3, а число пунктов назначения n=5. Следовательно, невырожденный опорный план задачи будет определяться числом заполненных маршрутов (ненулевых переменных) в количестве 5+3-1=7.
По рассматриваемому методу заполнение маршрутов начнем с клетки, стоящей в левом верхнем углу. Потребность в грузе пункта В1 составляет 60 ед и от поставщика А1 можно эту потребность полностью удовлетворить. Иначе, по маршруту А1В1 будет запланирована поставка в размере 60 ед. Следующий потребитель В2 нуждается в поставке 70 ед груза, что также можно выполнить, доставив требуемый объем груза от поставщика А1, у которого после первой поставки осталось 140-60=80 ед. Таким образом, по маршруту А1В2 можно запланировать доставку груза в полном объеме. Оставшийся у поставщика А1 объем груза в 10 ед запланируем доставить потребителю В3,
т.е. по маршруту А1В3. Так как ресурсы поставщика А1 полностью израсходованы, потребителю В2 оставшиеся 110 ед груза запланируем доставить по маршруту А2В3 , т.е. от поставщика А2. Пользуясь подобным алгоритмом, по маршруту А2В4 запланируем доставку 70 ед, по маршруту А3В4 доставку 60 ед и по маршруту А3В5 оставшиеся 100 ед груза (табл.17).
Таблица 17
Результирующая таблица опорного плана задачи 12
| Поставщик | Пункт назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребность |
Теперь рассчитаем суммарные затраты на доставку всего объема грузов:
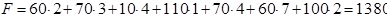
Остается только оценить полученный план. Он выглядит в матричной форме следующим образом:
 .
.
План имеет 7 заполненных маршрутов. Следовательно, полученный опорный план невырожденный, может быть проанализирован на оптимальность и при необходимости улучшен (см. ниже).
Метод минимального элемента. В методе северо-западного угла алгоритм заполнения маршрутов был построчный с учетом остатков груза у очередного поставщика, при этом полностью игнорировались размеры тарифных ставок на перевозки. Очевидно, что минимальная стоимость перевозок будет обеспечена в большей мере, если при заполнении соответствующих маршрутов (клеток) отдавать предпочтение маршрутам с минимальной тарифной ставкой на перевозку. В этом и заключается идея метода минимального элемента.
З а д а ч а 13. Повторим процедуру нахождения первичного опорного плана для сформулированной выше задачи, реализуя этот метод.
В общем наборе тарифов есть два маршрута со ставкой «1» и три маршрута со ставкой «2», два маршрута со ставкой «3», четыре маршрута со ставкой «4», два маршрута со ставкой «7», по одному маршруту со ставками «8» и «9». В такой же последовательности будем перераспределять груз. При равенстве тарифов маршрут выбирают произвольно.
Начнем с маршрута А2В5. Назначим объем перевозок по нему 100 ед, а по маршруту А2В3 оставшиеся у поставщика А2 80 ед груза. Естественно, маршруты А1В5 и А3В5, а также А2В1, А2В2, А2В4 должны быть выключены из списка свободных (знак Х). Теперь заполним маршрут А1В1 , назначив по нему перевозку груза в объеме 60 ед (таков запрос потребителя В1) и выведем из состава свободных маршрут А3В1. Следующим заполняем маршрут А1В4 количеством груза в объеме 80 ед (оставшиеся у поставщика А1 после заполнения маршрута А1В1). Соответственно исключаем маршруты А1В2, А1В3. Оставшиеся маршруты закрываем безвариантно (табл.18).
Таблица 18
Заполнение таблицы при методе минимального элемента
| Поставщик | Пункт назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | Х | Х | Х | |||
| А2 | Х | Х | Х | |||
| А3 | Х | Х | ||||
| Потребность |
В результате получаем следующий опорный план:
 ,
,
для которого функция цели принимает значение
 .
.
Полученный план имеет 7 заполненных маршрутов, поэтому план невырожденный и может быть в дальнейшем улучшен (если при первом шаге начать составление плана с маршрута А2В3, то получим план со значением функции цели F=1480).
Видим, что для данной задачи метод северо-западного угла дает более перспективный план.
Метод аппроксимации по Фогелю. В принципе этот метод является развитием идеи метода минимального элемента, т.е. заполнение маршрутов с учетом тарифных ставок.
З а д а ч а 14. Рассмотрим его на примере той же задачи. Правее столбцов и ниже строк записывают текущую разность между тарифными ставками незакрытых маршрутов как по строкам (справа), так и по столбцам (внизу). Разность определяется между двумя минимальными ставками. Из полученных разностей выбирается наибольшая по абсолютному значению и далее первым заполняется тот маршрут в данном столбце или строке, который имеет минимальную тарифную ставку. Если по какому-либо потребителю или поставщику полностью используются запасы или закрываются поставки, все остальные маршруты по данному направлению закрываются и прекращаются процедуры нахождения разностей по тарифам. В табл.19 представлены результаты поиска опорного плана по вышеописанной схеме.
Таблица 19
Нахождение опорного плана по Фогелю
| Склад | Потребитель | Запас | Разность по строкам | ||||||||||
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | Х | Х | Х | - | |||||||||
| А2 | Х | 1 120 | Х | Х | |||||||||
| А3 | Х | Х | |||||||||||
| Потреб- ность | |||||||||||||
| Разность по столбцам | |||||||||||||
| - | |||||||||||||
| - | - | ||||||||||||
| - | - | - | |||||||||||
| - | - | - | |||||||||||
В таблице соблюдался следующий порядок заполнения маршрутов: А1В1, А2В3, А3В5, А1В4, А2В2, А3В2, А3В4. Максимальные разности по столбцам и строкам выделены жирным шрифтом.
В результате получен следующий опорный план:
 ,
,
т.е. опорный план имеет 7 заполненных маршрутов, а, следовательно, он невырожденный. Функция цели принимает значение:
 .
.
Очевидно, наилучший опорный план получен по методу Фогеля, но и он может быть в дальнейшем улучшен (см. ниже).
6.3. Оценка опорного плана транспортной задачи на оптимальность
и нахождение очередного плана
Для нахождения оптимального плана применяется тот же общий принцип, что и при решении производственной задачи: первоначально находится опорный план, а затем методом последовательного его улучшения получают оптимальный план. Оценку и улучшение опорного плана проводят, пользуясь различными методами. Мы рассмотрим наиболее простой и часто применяемый – метод потенциалов. Но прежде чем рассмотреть его более подробно, заметим следующее. Если анализируемый опорный план вырожденный, то его следует превратить в невырожденный, включив в базис любой свободный маршрут (или несколько), назначив объем транспортируемого по нему груза в пренебрежимо малом объеме. В дальнейшем этот маршрут также должен участвовать во всех аналитических процедурах, но в матрицу оптимального плана он не включается.
Метод потенциалов. Первоначально ознакомимся со следующей теоремой.
Т е о р е м а. Если для некоторого опорного плана  , (i=1…m; j=1…n) транспортной задачи для каждого базисного маршрута существуют такие числа α1, α2, …, αm; β1, β2, …, βn, при которых
, (i=1…m; j=1…n) транспортной задачи для каждого базисного маршрута существуют такие числа α1, α2, …, αm; β1, β2, …, βn, при которых
 при хij >0
при хij >0
и 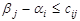 при
при 
для всех i=1…m и j=1…n, тогда  - оптимальный план задачи.
- оптимальный план задачи.
О п р е д е л е н и е. Числа αi и βj называются потенциалами соответственно пунктов отправления и пунктов потребления.
Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем.
Пусть одним из ранее рассмотренных методов найден опорный план. Следует предположение, что полученный план оптимален. Тогда для каждого из закрытых маршрутов можно определить потенциалы αi и βj (i=1…m, j=1…n). Эти числа находят, решая систему уравнений (полагаем, что хij >0):
 , (24)
, (24)
где сij – тариф соответствующего маршрута.
Так как количество определенных (базисных) маршрутов (n+m-1), а число неизвестных α,β равно (n+m), т.е. на единицу больше, то одно из неизвестных (обычно α1 или β1 ) приравнивают нулю, тогда легко считаются остальные по заполненным маршрутам опорного плана. После нахождения αi и βj для всех свободных маршрутов определяют числа
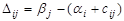 . (25)
. (25)
Если среди этих чисел нет положительных (хотя бы одного), то такой план считается оптимальным. В противном случае предположение относительно оптимальности анализируемого плана недействительно и его можно улучшить. Маршруты-претенденты на включение в базис будут иметь ∆ij >0. Но перевести в базис можно только один маршрут, для которого ∆ij>0 и max.
Заполнение такого маршрута неизбежно повлечет за собой изменение объемов поставок по другим маршрутам (естественно, так как любой опорный план всегда сбалансирован). Эта процедура выполняется на базе графического алгоритма, называемого циклом.
О п р е д е л е н и е. Циклом в таблице условий транспортной задачи называется замкнутая ломаная линия, начинающаяся из свободного маршрута, переводимого в базис, и имеющая в вершинах только занятые ранее маршруты, причем стороны ломаной линии лежат только в строках и столбцах (вертикально и горизонтально).
Примечание: линия цикла может проходить через заполненный маршрут сквозным направлением.
При правильном построении опорного плана для любого свободного маршрута можно построить только один цикл. После построения цикла следует перейти к новому опорному плану. Для этого надо переместить грузы в пределах маршрутов, связанных единым циклом, по следующему правилу.
1. Считая первым тот маршрут, который вносится в базис, присвоить ему знак «+» и далее, перемещаясь по циклу, следующему маршруту присваивается знак «-», далее опять знак «+» и так далее, т.е. всем нечетным маршрутам присваивается знак «+», а нечетным – знак «-» (только по концам линий цикла).
2. Среди маршрутов со знаком «-» выбирают маршрут с минимальным объемом перевозки.
3. По маршрутам со знаком «+» прибавляют вышеуказанный минимум грузоперевозки, а по маршрутам со знаком «-» это число отнимают. В результате получают очередной (также сбалансированный) опорный план.
4. Проверяют новый опорный план на оптимальность.
На рис.10 представлены некоторые варианты схем циклов при формировании очередного опорного плана транспортной задачи.

Рис. 10. Варианты  схем циклов
схем циклов
З а д а ч а 15. В качестве примера проанализируем опорный план выше рассмотренной задачи, полученный методом северо-западного угла. Для этого составим таблицу 20, где взамен обозначений поставщика Аi и потребителя Bj вписаны обозначения потенциалов αi и βj.
Таблица 20
Расчет потенциалов
| β1 = 2 | β2 = 3 | β3 = 4 | β4 = 7 | β5 = 2 | |
| α1 = 0 |
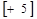
|

| |||
| α2 = 3 |

|

|

| ||
| α3 = 0 |

|

|

|
Первоначально рассчитаем потенциалы, воспользовавшись заполненными маршрутами. Составим систему из семи уравнений типа (24):
 ;
;  ;
; 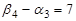 ;
;
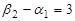 ;
;  ;
;  .
.
 ;
;
Так как в данном случае система имеет восемь неизвестных, т.е. на единицу больше количества уравнений, назначим 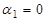 . Тогда получим значения потенциалов:
. Тогда получим значения потенциалов:
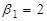 ;
;  ;
;  ;
;  ;
;  ;
;
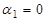 ;
;  ;
; 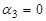 .
.
Полученные значения потенциалов внесем в табл.20. Теперь для каждого свободного маршрута рассчитаем значения ∆ij, согласно уравнения (25) и впишем их в таблицу (в квадратных скобках). Видим, что ∆ij>0 по двум маршрутам: А1В4 (∆ij=+5) и А3В3 (∆ij=+1). По всем остальным маршрутам этот параметр отрицательный. Очевидно, что маршрут А1В4 должен быть переведен из свободных в базисные.
Строим цикл. Он пройдет через следующие узловые маршруты:
А1В4→А2В4→А2В3→А1В3→А1В4.
Это единственный вариант построения ломаной, у которой в вершинах находятся заполненные (базисные) маршруты. Соответственно маршруты приобретают знаки:
А1В4→(+); А2В4→(-); А2В3→(+); А1В3→(-).
В цикле надо перемещать минимальное число, соответствующее транспортируемому грузу по маршруту со знаком «минус». Таковым будет число 10 по маршруту А1В3. Получим новый опорный план, представленный в табл.21.
Таблица 21
Первый улучшенный план
| β1 = 2 | β2 = 3 | β3 = -1 | β4 = 2 | β5 = -3 | |
| α1 = 0 |

|

| |||
| α2 = -2 |

|

|

| ||
| α3 = -5 |

|

|

|
Повторим относительно и этого плана описанные выше процедуры, получим значения потенциалов по всем маршрутам и видим, что и этот план неоптимален, так как имеет три маршрута с положительными потенциалами, равными (+1). С целью его улучшения введем в базис маршрут А3В3 (у него минимальная тарифная ставка) и строим цикл:
А3В3→А3В4→А2В4→А2В3→А3В3.
С учетом знаков по маршрутам объем перемещаемого по узловым точкам цикла груза в объеме 60 ед получаем очередной опорный план (табл.22).
Этот план также не может быть признан оптимальным, так как есть один маршрут (а именно А2В2), имеющий положительный потенциал. Приняв его
Таблица 22
Второй улучшенный план
| β1 = 2 | β2 = 3 | β3 = -1 | β4 = 2 | β5 = -2 | |
| α1 = 0 |

|

| |||
| α2 = -2 |

|

|

| ||
| α3 = -4 |
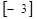
|

|
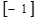
|
за план, перемещаемый в базис, и построив от него цикл
А2В2→А2В4→А1В4→А1В2→А2В2
с объемом перемещаемого груза в 70 ед, получим третий улучшенный опорный план, который представлен в табл.23.
Таблица 23
Третий улучшенный план
| β1 = 2 | β2 = 2 | β3 = -1 | β4 = 2 | β5 = -2 | |
| α1 = 0 |
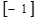
|

|

| ||
| α2 = -2 |

|
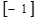
| |||
| α3 = -4 |
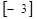
|
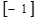
|
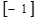
|
Этот план по всем незаполненным маршрутам имеет только отрицательные потенциалы. Следовательно, он оптимальный:
 .
.
Если просчитать функцию цели для всех рассмотренных планов, то получим следующий ряд:
 ;
;  ;
; 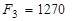 ;
;  ,
,
т.е. по сравнению с первоначальным вариантом оптимальный план улучшен примерно на 15%. Для этого выполнены четыре итерационных цикла оптимизации.
Поиск по сайту: