Определение оптимальных стратегий и цены игры и составляет сущность процесса нахождения решения игры

З а д а ч а 16. Рассчитать цену игры, заданную матрицей

,

из предположения, что игроки имеют оптимальные смешанные стратегии u^*=(0,3; 0,3; 0,4), z^*=(0,2; 0,5; 0,3).

Р е ш е н и е. Определим максимин и минимакс игры. Для этого выпишем вектор-строку минимальных выигрышей игрока А и максимальных проигрышей игрока В: α=(2; 3; 2), β=(5; 5; 4). Тогда максимин равен α_max =3, минимакс равен β_min=4. Следовательно, цена игры будет находиться между числами 3 и 4. Рассчитаем ее, воспользовавшись выражением (26).

.

Получили ответ – цена игры равна 3,63, что соответствует теоретическим представлениям.

Справедлива фундаментальная теорема Дж.Неймана, которую приведем без доказательства.

Т е о р е м а 2 (основная теорема матричных игр). Любая матричная игра имеет решение в смешанных стратегиях.

Значение и нетривиальность теоремы обусловлены тем, что в общем случае матричные игры в чистых стратегиях решения не имеют.

Т е о р е м а 3. Для того, чтобы число v было ценой игры, а u^* и z^* - оптимальными стратегиями, необходимо и достаточно выполнение неравенства:

; (j=1…n);

; (i=1…m).

Эта теорема определяет, что, соблюдая оптимальные смешанные стратегии, первый игрок может выиграть не менее цены игры, а второй игрок имеет шанс проиграть не более цены игры.

Т е о р е м а 4. Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш (или проигрыш второго) равен цене игры v независимо от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную (в том числе и чистые стратегии).

Она важна тем, что позволяет выработать методику решения игры для игр 2×2, 2×n, m×2.

Рассмотрим возможность приложения приведенных выше теорем для решения парной игры типа 2×2 аналитическим методом.

З а д а ч а 17. Найти решение игры, заданной матрицей

.

Р е ш е н и е. В данной задаче имеем две стратегии первого игрока, т.е. m=2, и две стратегии второго игрока, т.е. n=2. Прежде всего проверим, возможность наличия седловой точки в данной игре. Для этого выпишем минимальные выигрыши первого игрока по двум чистым стратегиям (по строкам) α=(2; 4) и максимальные проигрыши второго игрока также по его двум чистым стратегиям (по столбцам) β=(6; 5). Из этих векторов выпишем макcимин для первого игрока α_max=4, минимакс для второго игрока β_min=5. Так как они не равны, то решение следует искать в смешанных стратегиях, а цена игры должна быть в пределах .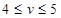

Предположим, что для игрока А стратегия задается вектором u=(u₁; u₂), а для игрока В – вектором z=(z₁; z₂). Тогда, на основании теоремы 4, при применении игроком В чистой стратегии z₁ или z₂ игрок А получит средний выигрыш, равный цене игры v, т.е.

(при стратегии z₁),

(при стратегии z₂).

Помимо двух записанных уравнений относительно u₁^* и u₂^* добавим уравнение, связывающее их как частоты:

.

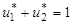Решая полученную систему трех уравнений с тремя неизвестными, находим

; ; .

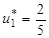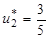Найдем теперь оптимальную стратегию для игрока В. В отношении его можно составить следующую систему уравнений:

(при стратегии u₁),

(при стратегии u₂),

.

Здесь имеются три уравнения, а неизвестных два, т.е. одно из уравнений уже лишнее. Решая систему, получаем

; .

Следовательно, решением задачи будут смешанные стратегии при цене игры:

; ; .

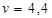Результаты полностью согласуются с теоретическими предпосылками.

Поиск по сайту: