 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачи нелинейного программирования
Выше рассматривался класс задач, характеризующихся двумя обстоятельствами:
- функцией цели  ,
,
- условиями ограничений, накладываемых на переменные
 .
.
Обе функции представляли собой линейные равенства (или неравенства, например, по ограничениям). Однако существует множество задач, для которых, во-первых, эти функции могут быть нелинейными, и, во-вторых, не обязательно наличие ограничений. Заметим принципиальную разницу в применимости принципа “оптимальности” к двум вышеуказанным типам функций:
- линейная функция (линия, плоскость) не имеет экстремума, т.е. ее
геометрические образы не имеют стационарных точек;
- нелинейная функция сама может иметь стационарные точки.
Поэтому становится понятным то различие в рассмотрении экстремальных задач в отношении типа функции цели. Кроме того, даже если при наличии линейной функции цели обязательные для нее ограничения описываются нелинейными функциями, то такая задача также не может уже рассматриваться как линейная.
Итак, если любая из функций F или gi(xj) представляет собой нелинейную функцию, то такая задача относится к области нелинейного программирования. Задача называется «с ограничениями», если существуют функции типа gi(xj), или «без ограничений», если таковые отсутствуют. В зависимости от постановки и содержания задачи нелинейного программирования (ЗНП) могут решаться в один прием, а в отдельных случаях их решение представляется в виде итерационного пошагового алгоритма. В последнем случае говорят, то данная задача относится к классу задач «динамического программирования».
Задача нелинейного программирования:
 ,
,
 (i=1…m),
(i=1…m),
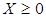 ,
,
где f и g – некоторые функции n переменных х1; х2;…; хn, в такой общей постановке не имеет универсального метода решения. Однако для отдельных классов задач, в которых сделаны дополнительные ограничения относительно свойств функций цели и ограничений, разработаны эффективные методы их решений. В частности, ряд таких методов имеется для решения ЗНП при условии, что функция цели – вогнутая (или выпуклая) функция, а область допустимых решений – выпуклая. Такие ограничения свойственны квадратичным функциям, в рамках которых и будут рассмотрены ниже приведенные методы решений ЗНП.
Поиск по сайту: