 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Расширенная задача и метод искусственного базиса
Для многих ЗЛП, записанных в форме основной задачи, среди векторов Рj не всегда есть необходимое количество единичных. Естественно, в таком случае описанные выше алгоритмы решения ЗЛП неприменимы. Однако путем некоторых преобразований можно получить приемлемое решение ЗЛП.
Рассмотрим такую задачу. Пусть требуется найти максимум функции

при условиях

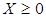
и среди векторов
 ,
, 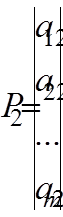 , …
, … 
нет m единичных.
О п р е д е л е н и е. Задача, состоящая в определении максимального значения функции

при условиях
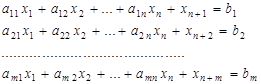 ,
,
где М – некоторое достаточно большое положительное число, конкретное значение которого обычно не задается, называется расширенной задачей по отношению к первичной ЗЛП.
Расширенная задача имеет опорный план
 ,
,
который определяется системой единичных векторов
 ,
,  , …,
, …,  .
.
Они и образуют базис m -мерного векторного пространства, который называется искусственным. Сами векторы (Рn+1, Pn+2, …,Pn+m) так же, как и переменные хn+i (i=1…m), называются искусственными. Так как расширенная задача имеет опорный план, то ее решение может быть найдено симплексным методом. Если в найденном оптимальном плане расширенной задачи значения искусственных переменных равны нулю и равны нулю все ∆j, то это означает, что получен оптимальный план исходной задачи. Рассмотрим особенности составления симплекс-таблицы для расширенной задачи на следующем примере.
З а д а ч а 7. Найти минимум функции  при условиях
при условиях
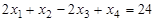 ,
,

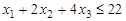 ,
,
 ,
,
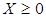 .
.
Р е ш е н и е. Запишем эту задачу в форме основной задачи: найти максимум функции  при условиях
при условиях
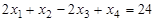 ,
,
 ,
,
 ,
,
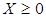 .
.
В системе уравнений рассмотрим векторы из коэффициентов при неизвестных:
 ,
, 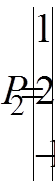 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Среди векторов-столбцов только два вектора – единичные, а для определения первого опорного плана и составления симплекс-таблицы необходимо иметь три таких вектора. Поэтому в левую часть третьего уравнения системы ограничений введем дополнительную неотрицательную переменную х7
и рассмотрим расширенную задачу, состоящую в максимизации функции цели  при условиях
при условиях
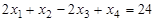 ,
,
 ,
,
 ,
,
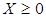 .
.
Эта расширенная задача имеет опорный план  , определяемый системой трех единичных векторов Р4, Р5, Р7. Составим симплекс-таблицу по вышеописанной методике, но добавим к ней еще одну строку, где записываются значения коэффициента kM (см. ниже).
, определяемый системой трех единичных векторов Р4, Р5, Р7. Составим симплекс-таблицу по вышеописанной методике, но добавим к ней еще одну строку, где записываются значения коэффициента kM (см. ниже).
Таблица 9
Симплекс-таблица к расширенной задаче 7
| i | Базис | Сб | Р0 | С1=2 | С2=-3 | С3=6 | С4=1 | С5=0 | С6=0 | С7=-М | ti |
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | Р7 | |||||
| Р4 | -2 | ||||||||||
| Р5 | 5,5 | ||||||||||
| Р7 | -М | -1 | -1 | 5,0 | |||||||
| zj | -2 | ||||||||||
| ∆j | -8 | ||||||||||
| kM | -10 | -1 | -2 |
Запишем расчетные выражения для определения элементов четвертой строки:
 ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
, 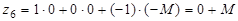 ,
,
 .
.
Видим, что каждое значение zj и функционала F0 состоят из двух слагаемых, одно из которых содержит М, а другое - нет. Аналогичное положение сохранится и после вычисления ∆j. Для удобства итерационного процесса после того, как будут выполнены расчеты по вышеуказанным двум строкам, множитель, состоящий при М, записывают в шестую строку, а слагаемое, которое не содержит М, - в четвертую или пятую строку соответственно.
В шестой строке по столбцам векторов Рj имеется два отрицательных числа (-1) и (-2). Наличие этих чисел говорит о том, что данный опорный план расширенной задачи не является оптимальным. Надо переходить к новому опорному плану. В базис следует ввести переменную х3, в свободные - переменную х7. Этот вектор не имеет смысла вводить ни в один из последующих базисов, поэтому в дальнейшем столбец данного вектора не заполняется.
Окончательное решение данной задачи получено на третьей итерации. Ниже представлена расчетная таблица для последующих итераций.
Таблица 10
Симплекс-таблица к задаче 7
| i | Базис | Сб | Р0 | С1=2 | С2=-3 | С3=6 | С4=1 | С5=0 | С6=0 | ti |
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | |||||
| Р4 | -1 | |||||||||
| Р5 | -1 | |||||||||
| Р3 | 1/2 | -1/2 | -1/2 | |||||||
| zj | -3 | -4 | ||||||||
| ∆j | -4 | |||||||||
| Р4 | 5/2 | 1/2 | ||||||||
| Р6 | -1/2 | 1/2 | ||||||||
| Р3 | 11/2 | 1/4 | 1/2 | 1/4 | ||||||
| zj | ||||||||||
| ∆j |
Как видно из табл.10, на второй стадии итерации имеем опорный план  . Разрешающим столбцом на этой стадии расчетов будет 10-й, а разрешающей строкой – вторая. Следовательно, в базис надо ввести переменную х6 взамен выводимой в свободные переменной х5. Следовательно, и второй опорный план не является оптимальным. На третьей стадии проверяется опорный план
. Разрешающим столбцом на этой стадии расчетов будет 10-й, а разрешающей строкой – вторая. Следовательно, в базис надо ввести переменную х6 взамен выводимой в свободные переменной х5. Следовательно, и второй опорный план не является оптимальным. На третьей стадии проверяется опорный план  . В результате расчетов в строке ∆j все элементы – неотрицательные числа. Следовательно, полученный план - оптимальный, функция цели принимает значение Fmax=68.
. В результате расчетов в строке ∆j все элементы – неотрицательные числа. Следовательно, полученный план - оптимальный, функция цели принимает значение Fmax=68.
Поиск по сайту: