 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Матричные игры и понятие седловой точки
Рассмотрим более подробно антагонистические игры и их основные свойства. Удобным способом задания игры двух участников с нулевой суммой является платежная матрица. Отсюда, кстати, происходит еще одно их название – матричные игры.
Предположим, имеется два игрока А и В. Они вступают в игру. У каждого из игроков на определенном этапе есть возможность выбора. Предположим также, что у каждого из игроков есть определенный набор стратегий:
игрок А → имеет m стратегий, т.е. i= (1… m);
игрок B → имеет n стратегий, т.е. j= (1… n).
Допустим, что при i -ой стратегии игрока A и j -ой стратегии игрока В результатом игры будет число аij, т.е. платеж. В результате, при реализации первым игроком всех m стратегий, а вторым - всех n стратегий по всем платежам можно составить матрицу игры:
 .
.

 Строки матрицы отражают платежи по отношению к первому игроку А (аij>0, если он выигрывает, аij<0, если проигрывает) при условии выполнения какой-то одной определенной стратегии (обозначим ее Аi) и при произвольных ответах второго игрока (стратегиях, которые можно обозначить как Вj). Столбцы отражают результаты игры для игрока А при условии, что второй игрок В будет придерживаться постоянства одной стратегии (т.е. Вj=const), а игрок А стратегию меняет.
Строки матрицы отражают платежи по отношению к первому игроку А (аij>0, если он выигрывает, аij<0, если проигрывает) при условии выполнения какой-то одной определенной стратегии (обозначим ее Аi) и при произвольных ответах второго игрока (стратегиях, которые можно обозначить как Вj). Столбцы отражают результаты игры для игрока А при условии, что второй игрок В будет придерживаться постоянства одной стратегии (т.е. Вj=const), а игрок А стратегию меняет.
Стратегия игрока, соответствующая строке игрока А или столбцу игрока В, называется чистой стратегией.
Матрицу А размерностью m  n называют конечной игрой размерностью m
n называют конечной игрой размерностью m  n.
n.
Классическим примером антагонистической игры является игра с двумя участниками, загадывающими независимо друг от друга числа. Предполагается, что если их сумма оказывается четной, то выигрыш, равный 1, достается первому игроку, а если нечетной, то второму. Положив, что для обоих игроков загадывание нечетного числа является первой стратегией, а четного – второй, можем записать платежную матрицу данной игры:
| В1(н/ч) | В2 (ч) | |
| A1 (н/ч) | -1 | |
| А2 (ч) | -1 |
Строки этой таблицы (матрицы) соответствуют стратегиям игрока А, столбцы - стратегиям игрока В, а ее элементы – результатам для первого игрока. Также из определения игры следует, что элементы данной матрицы, взятые с обратным знаком, соответствуют выигрышам второго игрока.
Более сложная и содержательная платежная матрица может быть получена, если несколько модифицировать предложенную игру. Допустим, что оба участника имеют право загадывать числа от 1 до 4 и это составляет их соответствующие стратегии (т.е. для каждого игрока имеется четыре стратегии). В случае, если результат сложения задуманных чисел будет четным, то второй игрок выплачивает первому получившуюся сумму, а если нечетным, то первый – второму. Запишем платежную матрицу для такой игры:
 .
.
К подобной форме может быть сведена модель, описывающая, например, соревнование двух фирм за вновь открывшийся рынок сбыта продукции и т.п.
Как уже отмечалось, важнейшим в теории игр является вопрос об оптимальности решения (выбора стратегии) для каждого из игроков. Проанализируем с этой точки зрения некоторую матричную игру, для которой задана платежная матрица 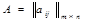 . При выборе i -ой стратегии игроком А его гарантированный доход независимо от действий игрока В составит α=min(aij), т.е. это минимальное число, стоящее в соответствующей строке при той или иной стратегии игрока В. Поскольку он может выбирать i -ю стратегию самостоятельно, то целесообразно этот выбор сделать таким, чтобы он при любой стратегии игрока В максимизировал величину гарантированного дохода, т.е. обеспечивал
. При выборе i -ой стратегии игроком А его гарантированный доход независимо от действий игрока В составит α=min(aij), т.е. это минимальное число, стоящее в соответствующей строке при той или иной стратегии игрока В. Поскольку он может выбирать i -ю стратегию самостоятельно, то целесообразно этот выбор сделать таким, чтобы он при любой стратегии игрока В максимизировал величину гарантированного дохода, т.е. обеспечивал
 .
.
Такой принцип выбора стратегии получил название “принцип максимина”. С другой стороны, аналогичные рассуждения могут быть проведены по поводу действий игрока В. Его наибольший проигрыш при переборе всех возможных стратегий составит β=max(aij). Следовательно, ему надо выбирать стратегию так, чтобы минимизировать величину проигрыша при любых действиях соперника, т.е. обеспечить
 .
.
Такой принцип выбора стратегии называется “ принцип минимакса ”. Логика игры позволяет утверждать, что всегда выполняется неравенство  . Особый интерес представляет случай, когда это неравенство становится равенством, т.е.
. Особый интерес представляет случай, когда это неравенство становится равенством, т.е.  . В этом случае говорят, что игра имеет седловую точку. Совпадение значений гарантированных выигрыша одного и проигрыша второго игроков при максиминной и минимаксной стратегии означает возможность достижения в игре некоторого оптимального (равновесного) состояния, от которого невыгодно отклоняться ни одному из игроков (т.е. не совершать ошибочных действий). Понятие “оптимальность” здесь означает, что ни один разумный (осторожный) игрок не будет стремиться изменить свою стратегию, так как его противник, в принципе, может этим воспользоваться и выбрать такую стратегию, которая даст худший для первого результат. Стратегии i* и j* , образующие седловую точку, называются оптимальными, а значение v=ai*j* называют ценой игры.
. В этом случае говорят, что игра имеет седловую точку. Совпадение значений гарантированных выигрыша одного и проигрыша второго игроков при максиминной и минимаксной стратегии означает возможность достижения в игре некоторого оптимального (равновесного) состояния, от которого невыгодно отклоняться ни одному из игроков (т.е. не совершать ошибочных действий). Понятие “оптимальность” здесь означает, что ни один разумный (осторожный) игрок не будет стремиться изменить свою стратегию, так как его противник, в принципе, может этим воспользоваться и выбрать такую стратегию, которая даст худший для первого результат. Стратегии i* и j* , образующие седловую точку, называются оптимальными, а значение v=ai*j* называют ценой игры.
Очевидно, что не всякая игра будет иметь седловую точку. Скорее наоборот, отсутствие седловой точки может быть правилом, а ее наличие – исключением. Примером игры, имеющей седловую точку, является игра с платежной матрицей:
 .
.
Запишем для игрока А вектор-строку минимальных выигрышей по всем трем его стратегиям (т.е. по трем строкам): α=(1; 5; -3). Для игрока В запишем вектор-строку из максимальных проигрышей по всем четырем его стратегиям (столбцам): β=(8; 10; 5; 17). Теперь запишем максимин для игрока А, т.е. максимальный выигрыш из минимально возможных: αmax=5, а для игрока В запишем значение минимакса, т.е. минимальный проигрыш из максимально возможных по всем его стратегиям: βmin=5. Видим, что в данном случае имеется седловая точка v= а23=5. Следовательно, для игры с приведенной выше матрицей решение игры будет: i=2; j=3; v=5 (для игрока А оптимальной будет вторая стратегия А2, для игрока В оптимальна третья стратегия В3, цена игры равна 5). При любом отклонении от оптимальной стратегии другой игрок будет иметь шанс “наказать” противника и выиграть больше цены игры (при ошибке игрока В) или проиграть меньше цены игры (при ошибке игрока А).
Поиск по сайту: