 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Программирования и физическая трактовка двойственной задачи
Все приведенные выше выкладки предполагали постоянство коэффициентов при переменных как в функции цели, так и в ограничениях, включая и постоянство свободных членов ограничений. Однако на практике эти условия могут выполняться кратковременно, либо вообще не выполняются. Поэтому возникает ряд проблем, например, при планировании, связанных с нарушением вышеуказанного принципа постоянства параметров ЗЛП. В связи с этим сформулируем несколько проблем:
- если для определенных условий проблемы найден оптимальный план
производства, то насколько он будет устойчив при изменении цен на гото-
вую продукцию;
- если найден оптимальный план, то как на него могут повлиять изменения
объемов ресурсных запасов;
Эти проблемы объединяются в одну – проблему параметрической устойчивости задачи линейного программирования.
Рассмотрим штатную ЗЛП по планированию производства: найти максимальное значение функции 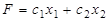 при условиях
при условиях
 ,
,
 ,
,
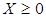 .
.
Так как ЗЛП имеет всего две переменные, выполним ее решение графическим методом. Предположим, что ее решение представляется рис. 7.

Рис.7. К обоснованию параметрической устойчивости задачи
линейного программирования
Ограничительные линии mn и pq графически отражают первое и второе неравенства-ограничения соответственно и совместно с осями координат (условия положительности переменных) образуют область допустимых решений (выделено на рис.7). Линия уровней a(0)b(0), проведенная через начало координат, имеет уравнение

и отвечает нулевому значению функции цели. Оптимальный план задачи  соответствует координатам вершины А многоугольника области допустимых решений (положение линии уровней a(1)b(1)), а максимальное значение функции цели будет равно
соответствует координатам вершины А многоугольника области допустимых решений (положение линии уровней a(1)b(1)), а максимальное значение функции цели будет равно  .
.
Теперь поставим вопрос: в каких пределах могут изменяться цены на продукцию при условии неизменности оптимального плана производства. Геометрически это означает следующее: в каких пределах может изменяться угол наклона линии уровней a(1)b(1) при ее вращении вокруг точки А. Очевидно, оно ограничивается углами α1 или α2, так какположение линии уровней ограничивается двумя ограничительными линиями - mn и pq. Но тангенс угла наклона линии mn можно найти из первого ограничения, записав его в виде уравнения
 ,
,
откуда он равен  .
.
Также, записав второе ограничение в виде уравнения
 ,
,
получим тангенс угла наклона линии pq равным  .
.
Так как тангенс угла наклона линии уровней рассчитывается по выражению 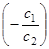 , то ответ на поставленный вопрос будет следующий: при постоянстве технологических нормативов и объемов сырьевых материалов оптимальный план и выручка от продажи продукции будут неизменными, если цены на продукцию, изменяясь, будут отвечать соотношениям:
, то ответ на поставленный вопрос будет следующий: при постоянстве технологических нормативов и объемов сырьевых материалов оптимальный план и выручка от продажи продукции будут неизменными, если цены на продукцию, изменяясь, будут отвечать соотношениям:

 ≤
≤ 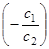 ≤
≤  .
.
Они определяют параметрическую устойчивость решения ЗЛП по ценам на продукцию. Равенства являются предельным состоянием, так как при его достижении задача не будет иметь однозначного решения по оптимальному плану.
Примечание: при любом относительном изменении цен значение функции цели будет также изменяться.
Рассмотрим кинетику изменения решения задачи при изменении объема сырьевых материалов. Предположим, при некотором первоначальном объеме (свободные члены в неравенствах-ограничениях имели значения b1 и b2) получено решение задачи и ее оптимальный план лежит в вершине В0, рис.8. Если значениям свободных членов в ограничениях дать приращение ∆b, то правомерно поставить вопрос:

Рис.8. К обоснованию параметрической устойчивости задачи линейного
программирования к объему сырьевых ресурсов
каким образом эти изменения повлияют на содержание оптимального плана. Геометрическая трактовка решения показывает, что приращение объемов сырьевых материалов вызовет соответствующий перенос ограничительных линий: например, линия mn переместится в положение m(1)n(1), а линия pq – в положение p(1)q(1). В зависимости от того, произойдут ли эти изменения порознь или одновременно, будем иметь еще дополнительно три варианта оптимальных планов, отвечающих координатам точек В1, В2, В3. Эти построения констатируют важный факт – с изменением свободных членов в ограничениях определенным образом будет меняться и функция цели, т.е правомерна запись  .
.
Из теории двойственности следует
Т е о р е м а: в оптимальном плане двойственной задачи значение переменной yi* численно равно частной производной функции  прямой задачи по данному аргументу, т.е.
прямой задачи по данному аргументу, т.е.
 .
.
Следовательно, изменение величин bi приводит к увеличению или уменьшению  и это изменение определяется величиной
и это изменение определяется величиной  . Отсюда вытекает, например, экономическая интерпретация оптимальных переменных двойственной задачи:
. Отсюда вытекает, например, экономическая интерпретация оптимальных переменных двойственной задачи:
каждая переменная yi может рассматриваться как предельная (мгновенная) оценка вклада i –го ресурса в cуммарный доход F при оптимальном решении Х*,
или:
величина yi равна приросту дохода, возникающему при увеличении i –го ресурса на единицу при условии оптимального использования ресурсов.
Переменные двойственной задачи имеют различные наименования. Например, они называются двойственными оценками, теневыми ценами, условными двойственными оценками и т.п. Л.В.Канторович предлагал такой термин, как объективно обусловленные оценки. Несмотря на возможные аналогии, двойственные оценки не следует однозначно отождествлять с ценами.
Учитывая специфический характер переменных двойственной задачи, на основе теории двойственности приведем некоторые выводы, имеющие практическую значимость в экономических исследованиях:
- если при подстановке параметров оптимального плана прямой задачи i -е ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей двойственной переменной равно нулю (это означает, что если некоторый ресурс bi имеется в избыточном количестве и не используется полностью при реализации оптимального плана, то i- е ограничение становится несущественным и объективно обусловленная оценка такого ресурса равна нулю);
- если при подстановке параметров оптимального плана двойственной задачи j- е ограничение выполняется как строгое неравенство, то оптимальное значение соответствующей переменной прямой задачи должно быть равно нулю (это означает, что объективно обусловленные оценки сырьевых материалов, используемых при производстве j -го продукта, завышены и его производство нерентабельно при существующей цене на данное изделие, а, следовательно, в оптимальном плане прямой задачи объем его выпуска будет равен нулю).
Заметим, что выводы, сделанные в соответствии с перечисленными выше пунктами, изменятся, если ввести коррективы в цены на продукцию. Направление таких изменений очевидно.
Рассмотрим вышеприведенные выводы на следующем примере.
З а д а ч а 11. Для производства трех видов изделий А,В,С, используется три различных вида сырьевых материалов, Каждый из видов сырья может быть использован в количестве, соответственно не большем, чем 180, 210 и 244 кг. Нормы затрат каждого из видов сырья на единицу продукции данного вида и стоимость единицы продукции каждого вида приведены в табл. 13. Определить план выпуска продукции, при котором полученная прибыль будет
Таблица 13
Технологическая программа производства к задаче 11
| Вид сырья | Нормы расхода сырья на одно изделие | Запас сырья | ||
| А | В | С | ||
| I | ||||
| II | ||||
| III | ||||
| Цена изделия | ||||
| План выпуска | х1 | х2 | х3 |
максимальной и оценить каждый из видов сырья, используемого для производства изделий.
Запишем первую часть задачи. Если план выпуска будет х1, х2, х3, то оптимальный план будет таким, когда будет максимальная прибыль, т.е. максимальной будет функция  при следующих условиях
при следующих условиях
 ,
,
 ,
,
 ,
,
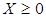 .
.
Запишем вторую часть задачи. Примем, что объективно обусловленная оценка каждого вида сырья будет соответственно равна y1, y2, y3. Тогда общая оценка сырья, используемого на производство всех изделий, будет равна
 и она должна быть минимальной. Запишем в виде неравенств условия соотношений объективно обусловленной стоимости сырья, пошедшего на изготовление каждого изделия, в сравнении с ценой данного изделия:
и она должна быть минимальной. Запишем в виде неравенств условия соотношений объективно обусловленной стоимости сырья, пошедшего на изготовление каждого изделия, в сравнении с ценой данного изделия:
 ,
,
 ,
,
 ,
,
 .
.
Видим, что эти записи соответствуют прямой и двойственной задачам. Решение прямой задачи определит оптимальный план выпуска, а решение двойственной задачи - оптимальную систему оценок сырьевой базы. Чтобы найти решение этих задач, следует сначала отыскать решение какой-либо одной из них. Наилучшим и более простым способом можно решить прямую задачу, так как она содержит неравенства типа “ ≤ ” и введение дополнительных переменных не усложнит процесс решения. В табл.14 представлено заключительное содержание итерационного процесса симплекс-метода.
Таблица 14
Итоговая симплекс-таблица к задаче 11
| i | Базис | Сб | Р0 | С1=10 | С2=14 | С3=12 | С4=0 | С5=0 | С6=0 | ti |
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | |||||
| Р2 Р5 Р3 zj ∆j | 19/8 23/8 -3/4 97/4 57/4 | 5/8 1/8 -1/4 23/4 23/4 | -1/8 -5/8 1/4 5/4 5/4 |
Имеем оптимальный план прямой задачи 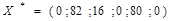 и значение функции цели
и значение функции цели 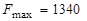 . Оптимальный план двойственной задачи будет
. Оптимальный план двойственной задачи будет  и соответственно значение функции цели
и соответственно значение функции цели  . Подставим значения оптимального плана прямой задачи в соответствующие неравенства и выполним необходимые расчеты:
. Подставим значения оптимального плана прямой задачи в соответствующие неравенства и выполним необходимые расчеты:
 → 180,
→ 180,
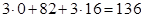 < 210,
< 210,
 → 244.
→ 244.
Расчеты показывают, что первый и третий типы сырьевых материалов полностью использованы для выполнения программы, а второй тип сырья использован не полностью, т.е. на предприятии он находится в избытке. Именно поэтому его обобщенная оценка (в двойственной задаче вторая переменная) равна нулю (см. вышеприведенные теоремы двойственности). Практически это означает, что любые изменения в объемах по второму сырьевому материалу совершенно не смогут повлиять на содержание оптимального плана производства.
Таким образом, положительную двойственную оценку имеют лишь те виды сырья, которые полностью используются при оптимальном плане производства изделий. Более того, оптимальный план двойственной задачи показывает, какой из использованных типов сырьевых материалов более перспективен с точки зрения увеличения суммарной прибыли (при соответствующем изменении оптимального плана). Видим, что увеличение количества сырья первого типа на единицу (например, на 1 кг) приведет к тому, что появится возможность найти новый оптимальный план производства изделий, при котором общая стоимость изготовляемой продукции возрастет на 5,75 руб. и это может быть достигнуто увеличением выпуска изделий типа В на 5/8 ед и сокращения выпуска изделий типа С на 1/4 ед. Вследствие этого уменьшится использование сырья третьего вида на 1/8 кг. Точно так же увеличение на 1 кг сырья третьего вида позволит найти новый оптимальный план производства, при котором общая стоимость изготовленной продукции возрастет на 1,25 руб. Это будет достигнуто в результате увеличения выпуска изделий типа С на 1/4 ед и уменьшения изготовления изделий типа В на 1/8 ед, причем объем используемого сырья второго вида возрастет на 5/8 кг.
При подстановке оптимальных оценок в систему ограничений двойственной задачи получаем
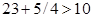 ,
,
 ,
,
 .
.
Первое ограничение двойственной задачи выполняется как строгое неравенство (см. теоремы двойственности). Это означает, что объективно обусловленная стоимость сырья, используемого при производстве одного изделия типа А, выше цены этого изделия, и, следовательно, выпускать это изделие невыгодно, что и отражено в оптимальном плане прямой задачи. Второе и третье ограничения двойственной задачи выполняются как строгие равенства. Это означает, что двойственная оценка сырьевых материалов, используемых при производстве изделий типа В и С хорошо сбалансирована с ценами. Поэтому выпускать эти два вида продукции целесообразно. Для того, чтобы в план производства вошли все три типа изделий, очевидно, необходимо увеличить стоимость изделия типа А и найти новый оптимальный план. Но двойственные оценки тесным образом связаны с оптимальным планом прямой задачи. Поэтому всякое изменение исходных данных прямой задачи может оказать влияние как на ее оптимальный план, так и на систему оптимальных двойственных оценок.
Принципы анализа ЗЛП на устойчивость, показанные на примере задачи с двумя переменными, полностью могут быть распространены и на более многомерные задачи. При этом качественные соотношения, усложняясь, сохранят свою структуру. Тем более очевидно, что с ростом размерности задачи выполнение такого анализа существенно усложняется, а порой становится невозможным. Однако в большинстве случаев надобность в выполнении анализа на устойчивость в прямой форме необязательна. Принцип двойственности позволяет существенно упростить процедуру такого анализа, но при этом следует отдавать отчет в том, что во многом результаты такого анализа будут носить качественный характер и нуждаются в трактовке применительно к физическому смыслу ЗЛП.
Поиск по сайту: