 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Геометрический метод решения игр
Cуществует очень простой и наглядный способ поиска оптимальных смешанных стратегий в матричных играх, где один из игроков имеет только две стратегии. Он основан на графическом представлении системы вышеприведенных уравнений.
Предположим, что игра задана матрицей

и игрок А имеет возможность выбирать между двумя стратегиями с вероятностями u1 и u2=1-u1, а игрок В имеет три чистые стратегии. Тогда, на основании теоремы 4, ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, примут вид
 ,
,
 ,
,
 .
.
Имеем три линейных уравнения 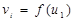 , которые могут быть представлены графически в виде линий с различными угловыми коэффициентами. Для этого на горизонтальной оси, например “ u1”, нанесем отрезок, равный единице, и возведем вертикали из начала и конца этого единичного отрезка (рис.11). На вертикалях построим числовые оси в единицах платежей игры. При u1=0 (что соответствует u2=1) на вертикальную ось нанесем числа, соответствующие выигрышам игрока А, если бы он играл вторую чистую стратегию (т.е. числа второй строки). При u1=1 (это соответствует u2=0)на вертикальную ось нанесем числа первой строки соответственно. Соединив числа aij, принадлежащие трем столбцам, т.е. чистым стратегиям второго игрока В, получаем линии функции
, которые могут быть представлены графически в виде линий с различными угловыми коэффициентами. Для этого на горизонтальной оси, например “ u1”, нанесем отрезок, равный единице, и возведем вертикали из начала и конца этого единичного отрезка (рис.11). На вертикалях построим числовые оси в единицах платежей игры. При u1=0 (что соответствует u2=1) на вертикальную ось нанесем числа, соответствующие выигрышам игрока А, если бы он играл вторую чистую стратегию (т.е. числа второй строки). При u1=1 (это соответствует u2=0)на вертикальную ось нанесем числа первой строки соответственно. Соединив числа aij, принадлежащие трем столбцам, т.е. чистым стратегиям второго игрока В, получаем линии функции 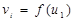 .
.

Рис. 11. Геометрический метод решения игры
Они отражают зависимости среднего выигрыша игрока А от значения вероятности u1, с которой он выбирает свою первую стратегию, для случаев, когда его противник применит первую, вторую или третью чистую стратегию. Итак, если из любой точки на отрезке u1=0…1 восстановить перпендикуляр, то ордината пересечения его с любой линией даст значение текущего выигрыша для игрока А, если он будет играть в соответствующих смешанных стратегиях u1 и u2=1-u1, а игрок В – только в соответствующих чистых стратегиях. Тогда значениям минимального гарантированного дохода первого игрока соответствует нижняя огибающая всех трех прямых. Согласно принципу максимина, оптимальному выбору игрока А будет соответствовать наивысшая точка, лежащая на данной огибающей, т.е. точка М. Зная ее, можно определить оптимальную смешанную стратегию первого игрока u*=(u1*; 1-u1*) и цену игры, равную v*.
Геометрическая интерпретация игры позволяет конкретизировать алгоритм ее аналитического решения. Из приведенных построений видно, что решение игры для игрока А следует искать как координаты точки пересечения двух прямых. Из этого факта следует очень важный вывод: если имеется матрица игры типа 2×n или m×2, то для игрока, имеющего более двух чистых стратегий, только две из них будут вещественными, остальные стратегии будут равны нулю.
З а д а ч а 18. Найти решение игры, заданной матрицей
 .
.
Р е ш е н и е. Для игрока А имеем две чистые стратегии А1 и А2, игрок В имеет три чистые стратегии В1, В2, В3. Так как один из игроков имеет две стратегии, используем графоаналитический метод решения задачи. Первоначально построим геометрическую трактовку игры для игрока А (используем ось “ u2”).

Рис.12. Геометрическая интерпретация задачи 18
При чистой стратегии А1 (u1=1, u2=0) первого игрока имеем три платежных выигрыша 2; 4; 3, если второй игрок будет при этом придерживаться соответственно чистых стратегий В1, В2, В3. Если же первый игрок будет играть чистую стратегию А2 (u1=0, u2=1), то он, в зависимости от стратегии второго игрока, получит выигрыш 5; 1; 4. Отложив эти выигрыши на соответствующих осях и соединив линиями значения выигрышей игрока А, возможные при соответствующих стратегиях игрока В, получим три прямых В1, В2, В3. Пользуясь принципом максимизации минимального выигрыша (максимин), для игрока А наилучшим является смешанная стратегия, отвечающая координатам точки М. Ясно также, что для игрока В, стремящегося минимизировать максимальный возможный проигрыш, ни при каких обстоятельствах (в данной, конечно, игре) нельзя пользоваться чистой стратегией В3. Следовательно, решение надо находить в смешанных стратегиях, полагая, что первый игрок имеет стратегии А1 и А2, а второй игрок имеет стратегии В1 и В2. Запишем систему уравнений для игрока А (на основании теоремы 4):
 ,
,
 ,
,
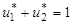 .
.
Решением игры для игрока А будет  при цене игры
при цене игры  .
.
Для игрока В при его игре в смешанных стратегиях и при известной цене игры базовая система уравнений будет иметь вид:
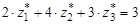 ,
,
 ,
,
 .
.
Имеем три уравнения и три неизвестных. Решением этой системы будет
 .
.
Видим, что и строго аналитическое решение задачи подтвердило сформулированный ранее вывод, полученный на основании графической интерпретации задачи – второй игрок может использовать (так же, как и первый) только две стратегии, остальные ни при каких обстоятельствах не должны применяться. В данном случае игрок В не должен использовать третью стратегию В3 (иначе он может проиграть больше минимакса).
З а д а ч а 19. Найти решение игры, заданной матрицей:
 .
.
Р е ш е н и е. В данной задаче для игрока А имеем три чистые стратегии А1, А2, А3, а игрок В имеет две чистые стратегии В1, В2. Так как один из игроков имеет две стратегии, решим задачу графоаналитическим методом. Но теперь применим его для игрока В, использовав горизонтальную ось “ z2”, рис.13 (так как В проигрывает, то на вертикальных осях числа имеют отрицательное значение).
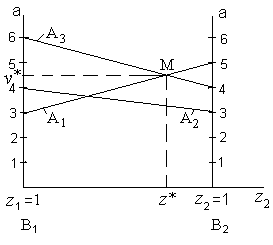
Рис.13. Геометрическая интерпретация задачи 19
При чистой стратегии В1 (z1=1, z2=0) второго игрока имеем три платежных проигрыша 3; 4; 6, если первый игрок будет придерживаться соответственно чистых стратегий А1, А2, А3. Если второй игрок будет играть чистую стратегию В2 (z1=0, z2=1), то он, в зависимости от стратегии первого игрока, проиграет 5; 3; 4. Отложив эти проигрыши на соответствующих осях и соединив линиями проигрыши игрока В при соответствующих стратегиях игрока А, получим три характеристических прямых А1, А2, А3. Элементарный анализ показывает, что цена игры в данной задаче будет находиться в пределах 4 ≤ v ≤ 5. Так как игрок В проигрывает, то он должен придерживаться принципа минимакса, т.е. ему необходимо обеспечить для себя минимально возможный из максимальных проигрышей. Этот принцип для него будет реализован, если он будет придерживаться смешанной стратегии, соответствующей точке М (рис.13). Тогда для чистых стратегий А1, А3 составим систему уравнений:
 ,
,
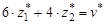 ,
,
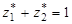 .
.
Решением игры для игрока В будет  при цене игры
при цене игры  .
.
Для игрока А при его игре в смешанных стратегиях и при известной цене игры система уравнений будет:
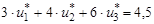 ,
,
 ,
,
 .
.
Имеем три уравнения и три неизвестных. Решением этой системы будет
 .
.
Мы снова получили подтверждение того, что у игрока, располагающего количеством стратегий более двух, в реальности остаются также только две стратегии.
Приведем пример того, как в реальной практике бизнеса можно применить положения теории игр.
З а д а ч а 20. Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Однако можно предположить, что его величина характеризуется комплексом факторов, которые могут быть каким-то образом формально объединены в виде трех состояний В1, В2, В3. С учетом этих обстоятельств анализируются три возможных варианта выпуска модели А1, А2, А3. Каждый из этих вариантов требует своих затрат и обеспечивает в конечном итоге различный эффект. Пробная реализация показала, что прибыль, например, в тыс. руб., которую получит предприятие при фиксированном объеме выпуска той или иной модели при соответствующем состоянии спроса, определяется матрицей (представим ее в виде таблицы):
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 |
Требуется найти стратегию поведения, которая позволит получить среднюю величину прибыли при любом состоянии спроса.
Р е ш е н и е. Любую задачу на игру следует начинать с проверки наличия седловой точки. Для рассматриваемой задачи поступим так же. Находим вектор минимальных выигрышей условного игрока А:
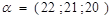
и вектор максимальных проигрышей условного игрока В:
 .
.
Пользуясь принципом максимина-минимакса, находим:
 ,
,  .
.
Имеем седловую точку, а соответственно решение задачи следующее: предприятию рекомендуется расширять производство модели А1 и реализовывать ее при любых вариантах спроса, тогда ему будет гарантирован доход в размере не менее 22 тыс. руб. (на условный объем партии).
Поиск по сайту: