 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Типы задач линейного программирования и их преобразование
Выше была рассмотрена одна из множества задач линейного программирования. В ней требовалось найти максимум линейной функции при условии, что ее переменные принимают неотрицательное значение и удовлетворяют некоторой системе линейных уравнений или неравенств. В общем виде это могут быть как неравенства, так и уравнения. В практике встречаются различные формы записи задач линейного программирования.
Определение 1. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
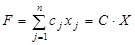 → max (min) (6)
→ max (min) (6)
при условии 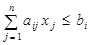
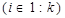 (7)
(7)
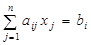
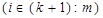 (8)
(8)
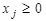
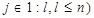 , (9)
, (9)
где аij, bi, cj - заданные постоянные величины, и k ≤ m.
Следовательно, общая ЗЛП может иметь функцию с любым видом находимого экстремума, а накладываемые ограничения могут иметь как неравенства, так и равенства.
Определение 2. Функция (6) называется целевой функцией (или функцией цели) задачи (6-9), а условия (7-9) – ограничениями данной задачи.
Определение 3. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции цели (6) при выполнении условий, когда ограничения – только неравенства типа (7) и на все неизвестные наложены требования неотрицательности, т.е. k=m, l=n.
Определение 4. Основной (или канонической) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции цели (6) при выполнении условий ограничений (8) и (9), где k=0, l=n, т.е. все ограничения только равенства при условии неотрицательности неизвестных.
Определение 5. Совокупность чисел Х=(х1, х2, …хn), удовлетворяющих условиям ограничений задачи (7), (8), (9), называется допустимым решением (или планом).
Определение 6. План Х*=(х1*, х2*, …, хп*), при котором функция цели (6) принимает экстремальное значение, называется оптимальным планом.
Значения целевой функции (6) при плане Х будем обозначать через F(X). Следовательно, если Х* - оптимальный план, то для любого Х ≠ Х* выполняется неравенство F(X) ≤ F(X*) или F(X) ≥ F(X*).
Указанные выше три формы задачи линейного программирования (общая, стандартная, основная) эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из ЗЛП, то тем самым может быть определен оптимальный план любой из трех вышеуказанных задач.
Чтобы перейти от одной формы записи ЗЛП к другой, нужно в общем случае уметь:
- сводить задачу минимизации функции цели к задаче максимизации;
- переходить от ограничений - неравенств к ограничениям – равенствам и
наоборот;
- заменять переменные, которые не подчинены условию неотрицательно-
сти.
Поясним эти положения.
1.В том случае, когда требуется найти минимум функции цели
 ,
,
можно перейти к нахождению максимума функции
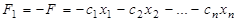 ,
,
так как 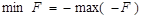 .
.
2.Ограничение-неравенство исходной ЗЛП, имеющее вид “ ≤ “, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной фиктивной неотрицательной переменной, а ограничение- неравенство вида “ ≥ “ - в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство
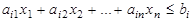
преобразуется в ограничение-равенство
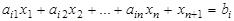 ,
,
где 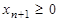 .
.
Соответственно, ограничение-неравенство
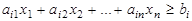
преобразуется в ограничение-равенство вида
 .
.
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств. Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной ЗЛП отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной (т.е. когда неравенство типа “ ≤ “ преобразуется в равенство), равно объему неиспользуемого соответствующего ресурса.
Функция цели при таких преобразованиях не меняет своего вида, так как для вновь вводимых переменных ценовые коэффициенты сj равны нулю.
3. В отдельных случаях целесообразно ограничения-равенства преобразовать в неравенства. Для этого из уравнения-ограничения надо выделить какую-либо переменную (обычно это удобно сделать с переменной, при которой ценовой коэффициент с равен единице), выразить ее через оставшиеся и в таком виде ввести в функцию цели. Затем из соответствующего уравнения-ограничения выделенную переменную удаляют и уравнение преобразуется в неравенство. В результате получают новый набор ограничений и новый вид функции с учетом пересмотра характера ограничений.
4. Если переменная хk не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными
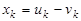 .
.
5. Для ЗЛП свойственна ситуация, когда число неизвестных больше числа уравнений ограничения. В этом случае говорят о степени неопределенности системы. Например, имеем систему из r – линейно независимых уравнений ограничения, а количество неизвестных n. Если r=n – система имеет единственное решение, т.е. является определенной. Если r<n, то задача (с точки зрения классических положений математического анализа) имеет бесчисленное множество решений, т.е. является неопределенной, причем p=(n-r) – степень неопределенности системы. Из этих двух случаев наиболее характерным является второй случай. Целью решения ЗЛП является нахождение из бесчисленного множества решений такого, которое удовлетворяло бы принципу экстремальности.
Примечание: в ограничениях ЗЛП нельзя производить какие-либо математические преобразования (например, умножать или делить на множители, производить сокращения и т.д.).
Задача 2. Записать в форме основной ЗЛП следующую задачу: найти максимум функции 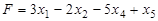 при условиях
при условиях
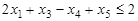 ,
,
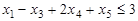 ,
,
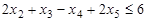 ,
,
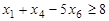 ,
,
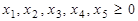 .
.
Р е ш е н и е. В данной задаче требуется найти максимум функции, а система ограничений содержит четыре неравенства (ограничения по неотицательности во внимание не принимаются). Следовательно, она записана в форме стандартной задачи и имеет степень неопределенности системы р=1. Чтобы записать ее в форме основной задачи, нужно перейти от ограничений-неравенств к ограничениям–равенствам. Так как число неравенств, входящих в систему ограничений, равно четырем, то этот переход может быть осуществлен введением четырех дополнительных неотрицательных переменных. При этом к левым частям каждого из неравенств вида “ ≤ “ соответствующая дополнительная переменная прибавляется, а из левых частей каждого из неравенств вида “ ≥ “ вычитается и ограничения принимают вид уравнений:
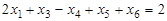 ,
,
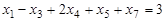 ,
,
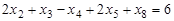 ,
,
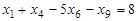 ,
,
 .
.
В результате степень неопределенности системы стала равна р=5.
Задача 3. Записать задачу, состоящую в минимизации функции
 при условиях
при условиях
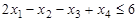 ,
,
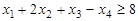 ,
,
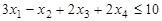 ,
,
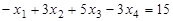 ,
,

в форме основной задачи линейного программирования.
Р е ш е н и е. В данной задаче требуется найти минимум целевой функции, а система ограничений содержит три неравенства и одно равенство, т.е. она записана в общей форме ЗЛП и степень неопределенности задачи р=0. Следовательно, чтобы записать ее в форме основной задачи, вместо нахождения минимума функции F нужно найти максимум функции F1 = - F при ограничениях, переписанных в форме равенств. Тогда исходная задача принимает следующий вид: найти максимум функции  при условиях
при условиях
 ,
,
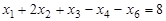 ,
,
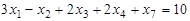 ,
,
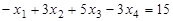 ,
,
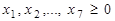 .
.
Получили ЗЛП в основной форме, степень неопределенности которой р=3.
Как будет показано ниже, весьма подробно разработаны методы решения ЗЛП, записанных в основной форме. Но иногда решение можно получить достаточно просто и в случае, если ЗЛП записана в стандартной форме. Проиллюстрируем это на следующем примере.
Задача 4. Записать в форме стандартной ЗЛП следующую задачу: найти максимум функции 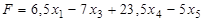 при следующих условиях
при следующих условиях
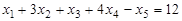 , (а)
, (а)
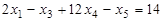 , (в)
, (в)
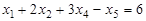 , (с)
, (с)
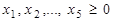 .
.
Р е ш е н и е. Исходная ЗЛП записана в форме основной задачи, имеет пять неизвестных и степень неопределенности р=2. Введя частные индексы по уравнениям-ограничениям, выполним процедуры по избавлению от ряда неизвестных. Методом последовательного исключения (см. ниже) приведем ограничения-равенства (а), (в), (с) к следующему виду:
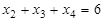 , (d)
, (d)
 , (e)
, (e)
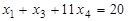 , (f)
, (f)
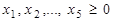 .
.
Уравнения получены по следующей схеме подстановок:
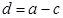 ,
,

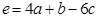 ,
,
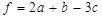 .
.
Из уравнений (d),(e),(f) выразим переменные х1, х2, х5 через переменные х3 и х4:
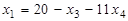 ,
,
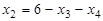 ,
,
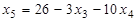
и, подставив их значения в функцию цели, получим новый вид функции
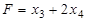 .
.
Теперь, если из уравнений (d), (e), (f) вывести переменные х1, х2, х5, они превращаются в ограничения –неравенства. Тогда первичная задача будет представлена так: найти максимум функции 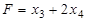 при условиях
при условиях
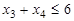 ,
,
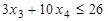 ,
,
 ,
,
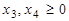 .
.
Заметим, что в такой редакции ЗЛП уже имеет две переменные взамен исходных пяти. Такого типа ЗЛП достаточно легко может быть решена графическим методом (см. ниже), что значительно упрощает процесс решения.
Из вышеприведенных примеров видно, что наиболее компактной является запись ЗЛП в стандартной форме и степень неопределенности задачи в этой форме записи ниже. Однако при количестве неизвестных более двух решение таких задач имеет большие методологические трудности.
Поиск по сайту: