 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нахождение решений двойственных задач
Практическая ценность наличия пары двойственных задач многозначна. Прежде всего с точки зрения методики решения ЗЛП приемнение двойственной задачи позволяет в отдельных случаях упростить решение и в частности свести его к графическому построению. Например, если:
а) количество неизвестных в прямой задаче более двух;
б) количество ограничений в прямой задаче равно двум,
то такая задача не может быть решена графически. Однако она будет иметь двойственную задачу типа:
а) количество неизвестных в двойственной задаче равно двум;
б) количество ограничений в двойственной задаче более двух,
и такая задача может быть решена графическим методом. Однако в этом случае можно получить только значение функции цели, но оптимальный план прямой задачи получить таким методом нельзя.
Независимо от структуры задач как прямой, так и двойственной, имеется возможность, решая первую, получить одновременно решение и второй. Не останавливаясь на теоретических положениях, рассмотрим методику поиска решений двойственной пары. Для этого рассмотрим следующий пример.
З а д а ч а 10. Для задачи, состоящей в определении максимального значения функции 
при условиях  ,
,
 ,
,
 ,
,
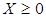 .
.
Составить двойственную задачу и найти ее решение.
Заметим, что эта задача уже рассматривалась выше при обосновании метода решения ЗЛП с помощью симплекс-таблицы (см. задачу 5).
Р е ш е н и е. Двойственная задача по отношению к исходной состоит в нахождении минимума функции 
при шести ограничениях 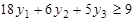 ,
,
 ,
,
 ,
,
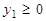 ,
,  ,
,  .
.
Воспроизведем конечную симплекс-таблицу решения прямой задачи.
Таблица 12
Симплекс-таблица к задаче 10
| i | Базис | Сб | Р0 | С1=9 | С2=10 | С3=16 | С4=0 | С5=0 | С6=0 | ti |
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | |||||
| Р2 Р3 Р6 zj ∆j | 1/4 5/4 | 1/9 -1/18 -1/6 2/9 2/9 | -1/6 5/24 -1/8 5/3 5/3 |
Прямая задача на первом этапе имела три единичных вектора Р4, Р5, Р6, (т.е. в базис входили переменные х4, х5, х6). Заметим также, что количество базисных переменных при решении прямой задачи всегда равно количеству ограничений, а соответственно всегда равно количеству неизвестных в двойственной задаче.
Как известно, прямая задача имела оптимальный план Х*=(0;8;20;0;0;96), а функция цели принимала значение
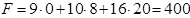 .
.
Двойственная задача будет иметь следующее решение:
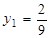 ,
,  ,
,  ,
,
а функция цели будет равна:
 .
.
П р а в и л о. Если среди векторов Р1; Р2; …; Рn+k, составленных из коэффициентов при неизвестных в системе уравнений в прямой задаче имеется m единичных, то оптимальный план двойственной задачи – это значения чисел zj в столбцах первичных единичных векторов, а функция цели двойственной задачи равна значению функции цели прямой задачи.
Для рассмотренной задачи:
 ,
,  ,
,  ,
,
чьи числовые значения в табл.12 выделены жирно.
Поиск по сайту: